
已知点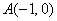 ,
,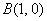 ,动点
,动点 的轨迹曲线
的轨迹曲线 满足
满足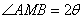 ,
,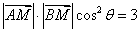 ,过点
,过点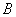 的直线交曲线
的直线交曲线 于
于 、
、 两点.
两点.
(1)求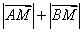 的值,并写出曲线
的值,并写出曲线 的方程;
的方程;
(2)求△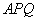 面积的最大值.
面积的最大值.
(1)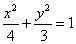
(2)△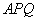 面积的最大值为3,此时直线
面积的最大值为3,此时直线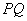 的方程为
的方程为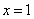 .
.
解析试题分析:解:(1)设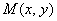 ,在△
,在△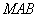 中,
中,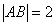 ,
,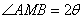 ,根据余弦定理得
,根据余弦定理得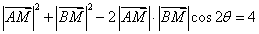 . (2分)
. (2分)
即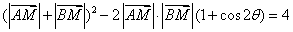 .
.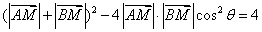 .
.
而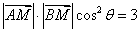 ,所以
,所以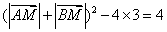 .
.
所以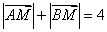 . (4分)
. (4分)
又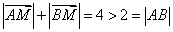 ,
,
因此点 的轨迹是以
的轨迹是以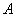 、
、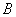 为焦点的椭圆(点
为焦点的椭圆(点 在
在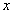 轴上也符合题意),
轴上也符合题意),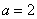 ,
,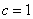 .
.
所以曲线 的方程为
的方程为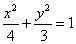 . (6分)
. (6分)
(2)设直线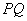 的方程为
的方程为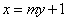 .
.
由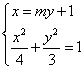 ,消去x并整理得
,消去x并整理得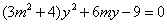 . ①
. ①
显然方程①的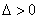 ,设
,设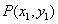 ,
,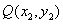 ,则
,则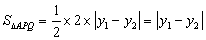
由韦达定理得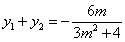 ,
,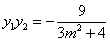 . (9分)
. (9分)
所以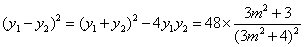 .
.
令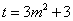 ,则
,则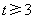 ,
,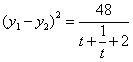 .
.
由于函数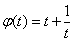 在
在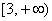 上是增函数.
上是增函数.
所以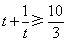 ,当
,当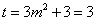 ,即
,即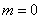 时取等号.
时取等号.
所以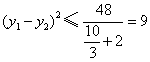 ,即
,即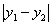 的最大值为3.
的最大值为3.
所以△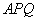 面积的最大值为3,此时直线
面积的最大值为3,此时直线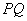 的方程为
的方程为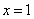 . (12分)
. (12分)
考点:直线与椭圆的位置关系
点评:解决的关键是根据椭圆的定义求解轨迹方程,同时结合直线与椭圆方程来联立方程组来求解最值,属于基础题。


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:
已知点![]() 是⊙
是⊙![]() :
:![]() 上的任意一点,过
上的任意一点,过![]() 作
作![]() 垂直
垂直![]() 轴于
轴于![]() ,动点
,动点![]() 满足
满足![]() 。
。
(1)求动点![]() 的轨迹方程;
的轨迹方程;
(2)已知点![]() ,在动点
,在动点![]() 的轨迹上是否存在两个不重合的两点
的轨迹上是否存在两个不重合的两点![]() 、
、![]() ,使
,使![]() (O是坐标原点),若存在,求出直线
(O是坐标原点),若存在,求出直线![]() 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省高三上学期第三次月考理科数学卷 题型:解答题
(本题满分14分)
已知点 是⊙
是⊙ :
: 上的任意一点,过
上的任意一点,过 作
作 垂直
垂直 轴于
轴于 ,动点
,动点 满足
满足 。
。
(1)求动点 的轨迹方程;
的轨迹方程;
(2)已知点 ,在动点
,在动点 的轨迹上是否存在两个不重合的两点
的轨迹上是否存在两个不重合的两点 、
、 ,使
,使 (O是坐标原点),若存在,求出直线
(O是坐标原点),若存在,求出直线 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源:2013届天津市高二第一学期期末理科数学试卷 题型:解答题
已知点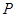 是⊙
是⊙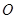 :
: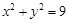 上的任意一点,过
上的任意一点,过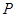 作
作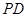 垂直
垂直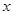 轴于
轴于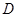 ,动点
,动点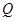 满足
满足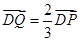 。
。
(1)求动点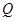 的轨迹方程;
的轨迹方程;
(2)已知点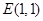 ,在动点
,在动点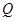 的轨迹上是否存在两个不重合的两点
的轨迹上是否存在两个不重合的两点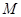 、
、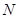 ,使
,使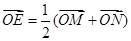 (O是坐标原点),若存在,求出直线
(O是坐标原点),若存在,求出直线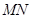 的方程,若不存在,请说明理由
的方程,若不存在,请说明理由
查看答案和解析>>
科目:高中数学 来源:2010年黑龙江省高二上学期期中考试数学理卷 题型:解答题
(本题10分) 已知点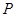 是⊙
是⊙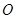 :
: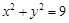 上的任意一点,过
上的任意一点,过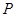 作
作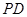 垂直
垂直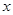 轴于
轴于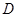 ,动点
,动点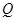 满足
满足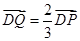 。
。
(1)求动点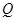 的轨迹方程;
的轨迹方程;
(2)已知点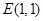 ,在动点
,在动点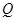 的轨迹上是否存在两个不重合的两点
的轨迹上是否存在两个不重合的两点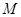 、
、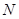 ,使
,使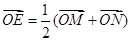 (O是坐标原点),若存在,求出直线
(O是坐标原点),若存在,求出直线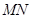 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分14分)
已知点![]() 是⊙
是⊙![]() :
:![]() 上的任意一点,过
上的任意一点,过![]() 作
作![]() 垂直
垂直![]() 轴于
轴于![]() ,动点
,动点![]() 满足
满足![]() 。
。
(1)求动点![]() 的轨迹方程;
的轨迹方程;
(2)已知点![]() ,在动点
,在动点![]() 的轨迹上是否存在两个不重合的两点
的轨迹上是否存在两个不重合的两点![]() 、
、![]() ,使
,使![]() (O是坐标原点),若存在,求出直线
(O是坐标原点),若存在,求出直线![]() 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com