
已知![]() ,其中
,其中![]() ,
,![]() .
.
(1)求f(x)的最小正周期;
(2)求f(x)的单调递增区间;
(3)f(x)的图象可由正弦函数的图象经过怎样的变换得到?
考点:
复合三角函数的单调性;平面向量数量积的坐标表示、模、夹角;三角函数的周期性及其求法.
专题:
综合题.
分析:
(1)由向量的坐标运算可求得f(x)=![]() •
•![]() =2sin(2x﹣
=2sin(2x﹣![]() ),从而可求得其周期;
),从而可求得其周期;
(2)由正弦函数的单调性可由2kπ﹣![]() ≤2x﹣
≤2x﹣![]() ≤2kπ+
≤2kπ+![]() ,k∈Z求得f(x)的单调递增区间;
,k∈Z求得f(x)的单调递增区间;
(3)利用三角函数的图象变换规律,可先进行相位变换,再进行周期变换,最后进行振幅变换即可.
解答:
解:(1)∵![]() =(sin2x,﹣
=(sin2x,﹣![]() ),
),![]() =(1,cos2x),
=(1,cos2x),
∴f(x)=![]() •
•![]() =sin2x﹣
=sin2x﹣![]() cos2x=2sin(2x﹣
cos2x=2sin(2x﹣![]() ),
),
∴f(x)的最小正周期T=![]() =π;
=π;
(2)由2kπ﹣![]() ≤2x﹣
≤2x﹣![]() ≤2kπ+
≤2kπ+![]() ,k∈Z得:
,k∈Z得:
kπ﹣![]() ≤x≤kπ+
≤x≤kπ+![]() ,k∈Z
,k∈Z
∴f(x)的单调递增区间为[kπ﹣![]() ,kπ+
,kπ+![]() ],k∈Z.
],k∈Z.
(3)y=sinx![]() y=sin(x﹣
y=sin(x﹣![]() )
)![]() y=sin(2x﹣
y=sin(2x﹣![]() )
)![]() y=2sin(2x﹣
y=2sin(2x﹣![]() ).
).
点评:
本题考查平面向量数量积的坐标表示,考查三角函数的周期性及其求法,考查正弦函数的单调性及三角函数的图象变换,属于中档题.


科目:高中数学 来源:2013届甘肃省高二3月月考数学试卷(解析版) 题型:解答题
(本小题满分14分)
已知函数 其中实数
其中实数 。
。
(1)若a=-2,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)若 在x=1处取得极值,试讨论
在x=1处取得极值,试讨论 的单调性。
的单调性。
查看答案和解析>>
科目:高中数学 来源:2010年湖南省高一上学期期中考试数学卷 题型:解答题
(满分10分)
已知 ,其中
,其中 为常数
为常数
(1)判断 在定义域上的单调性并用单调性的定义证明之;
在定义域上的单调性并用单调性的定义证明之;
(2)若函数的定义域为 ,求函数的最大值和最小值.
,求函数的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源:2010年江苏省高一第二次学情调研数学卷 题型:解答题
(本题满分15分)
已知函数 其中
其中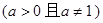 ,
,
设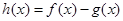 .
.
(1)求函数 的定义域,判断
的定义域,判断 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)若 ,求使
,求使 成立的
成立的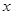 的集合
的集合
查看答案和解析>>
科目:高中数学 来源:2010-2011年江苏省盐城市高二下学期期中考试理科数学 题型:解答题
、(本题满分16分)
已知函数 ,其中
,其中 ..
..
(1)当 满足什么条件时,
满足什么条件时, 取得极值?
取得极值?
(2)已知 ,且
,且 在区间
在区间 上单调递增,试用
上单调递增,试用 表示出
表示出 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com