
���� ��1��������֪�������a��b���������ԲC�ķ��̣�
��2��AB��y=k1x+1������$\frac{{|{{k_1}-1}|}}{{\sqrt{1+k_1^2}}}=r$�������$��{1-{r^2}}��k_1^2-2{k_1}+1-{r^2}=0$��ֱ��AD��y=k2x+1��ͬ����$��{1-{r^2}}��k_2^2-2{k_2}+1-{r^2}=0$���Ƴ�k1��k2�Ƿ��̣�1-r2��k2-2k+1-r2=0����ʵ������k1•k2=1�����ǵ�r��1ʱ��D����Բ���¶��㣬B��������Բ���϶��㣬��BD�������㣬����붨����y���ϣ�����ֱ������Բ���̣������ص�����꣬���ֱ��BD�ķ��̣��Ƴ�ֱ��BD�����㣮
��� �⣺��1��������֪��$\frac{c}{a}=\frac{{\sqrt{3}}}{2}$��$\frac{1}{2}��2a��2b=4$����a2-b2=c2��
���a=2��b=1��
��������ԲC�ķ�����$\frac{x^2}{4}+{y^2}=1$��
��2��AB��y=k1x+1������$\frac{{|{{k_1}-1}|}}{{\sqrt{1+k_1^2}}}=r$�������$��{1-{r^2}}��k_1^2-2{k_1}+1-{r^2}=0$��
����ֱ��AD��y=k2x+1��ͬ����$��{1-{r^2}}��k_2^2-2{k_2}+1-{r^2}=0$��
����k1��k2�Ƿ��̣�1-r2��k2-2k+1-r2=0����ʵ������k1•k2=1��
���ǵ�r��1ʱ��D����Բ���¶��㣬B��������Բ���϶��㣬��BD�������㣬����붨����y���ϣ�
��$\left\{{\begin{array}{l}{y={k_1}x+1}\\{\frac{x^2}{4}+{y^2}=1}\end{array}}\right.$����$��{4k_1^2+1}��{x^2}+8{k_1}x=0$��������$B��{\frac{{-8{k_1}}}{4k_1^2+1}��\frac{-4k_1^2+1}{4k_1^2+1}}����D��{\frac{{-8{k_2}}}{4k_2^2+1}��\frac{-4k_2^2+1}{4k_2^2+1}}��$��
ֱ��BD��б��Ϊ${k_{BD}}=\frac{{{k_1}+{k_2}}}{-3}$��
ֱ��BD�ķ���Ϊ$y-\frac{-4k_1^2+1}{4k_1^2+1}=\frac{{{k_1}+{k_2}}}{-3}��{x-\frac{{-8{k_1}}}{4k_1^2+1}}��$��
��x=0����$y=\frac{-4k_1^2+1}{4k_1^2+1}+\frac{{{k_1}+{k_2}}}{-3}•\frac{{8{k_1}}}{4k_1^2+1}=\frac{20k_1^2+5}{{-3��{4k_1^2+1}��}}=-\frac{5}{3}$��
��ֱ��BD������$��{0��-\frac{5}{3}}��$��
���� ���⿼����Բ�ļ�������Բ���̵���ֱ������Բ��λ�ù�ϵ���ۺ�Ӧ�ã�ֱ�ߺ���������⣬����ת��˼���Լ�����������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
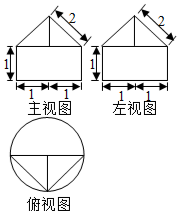 һ�������������ͼ��ͼ��ʾ����ü���������Ϊ��������
һ�������������ͼ��ͼ��ʾ����ü���������Ϊ��������| A�� | 2��+$\frac{\sqrt{3}}{3}$ | B�� | ��+$\frac{\sqrt{3}}{3}$ | C�� | 2��+$\frac{\sqrt{3}}{3}$ | D�� | ��+$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | M=P | B�� | P��M | C�� | N��P��∅ | D�� | M��N��∅ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com