
求证:![]() .
.
思路解析:比较已知条件和结论,发现结论中没有出现角θ,所以首先要消去它.然后由式子的结构特点,将切化弦统一函数名后分析比较不难得到结论.
证明:因为(sinθ+cosθ)2-2sinθ·cosθ=1,
将已知代入上式得4sin2α-2sin2β=1. ①
另一方面,要证![]() ,
,
即证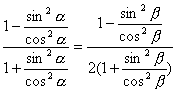 ,
,
即证cos2α-sin2α=![]() (cos2β-sin2β),
(cos2β-sin2β),
即证1-2sin2α=![]() (1-2sin2β),
(1-2sin2β),
即证4sin2α-2sin2β=1.
由于上式与①式相同,于是问题得证.
深化升华 在解决问题时,我们经常把综合法和分析法结合起来使用:根据条件的结构特点去转化结论,得到中间结论Q;根据结论的结构特点转化条件,得到中间结论P.若由P可以推出Q成立,就可以证明结论成立.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| 2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| 4 |
| 5 |
| 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com