
已知函数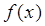 =ax2+(b-8)x-a-ab , 当x
=ax2+(b-8)x-a-ab , 当x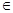 (-∞,-3)
(-∞,-3)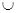 (2,+∞)时,
(2,+∞)时, 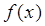 <0,当x
<0,当x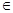 (-3,2)时
(-3,2)时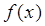 >0 .
>0 .
(1)求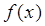 在[0,1]内的值域.
在[0,1]内的值域.
(2)若ax2+bx+c≤0的解集为R,求实数c的取值范围.
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:022
已知y=Ax2+Bx+C中A, B, C∈{0,1,2,…,9}, 且A, B, C中恰有一个为奇数. 则这样的二次函数共有__________(A, B, C互不相同).
查看答案和解析>>
科目:高中数学 来源:天津市新人教A版数学2012届高三单元测试39:微积分基本定理及应用 题型:044
已知y=ax2+bx通过点(1,2),与y=-x2+2x有一个交点x1,且a<0.如下图所示:

(1)求y=ax2与y=-x2+2x所围的面积S与a的函数关系.
(2)当a,b为何值时,S取得最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题总分14分)已知函数![]() =ax2+x-3,g(x)=-x+4lnx
=ax2+x-3,g(x)=-x+4lnx
h(x)=![]() -g(x)
-g(x)
(1)当a=1时,求函数h(x)的极值。
(2)若函数h(x)有两个极值点,求实数a的取值范围。
(3)定义:对于函数F(x)和G(x),若存在直线l:y=kx+b,使得对于函数F(x)和
G(x)各自定义域内的任意x,都有F(x)≥kx+b且G(x)≤kx+b成立,则称直线l:y=kx+b为函数F(x)和G(x)的“隔离直线”。则当a=1时,函数![]() 和g(x)是否存在“隔离直线”。若存在,求出所有的“隔离直线”。若不存在,请说明理由。
和g(x)是否存在“隔离直线”。若存在,求出所有的“隔离直线”。若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数![]() =ax2+(b-8)x-a-ab , 当x
=ax2+(b-8)x-a-ab , 当x![]() (-∞,-3)
(-∞,-3)![]() (2,+∞)时,
(2,+∞)时, ![]() <0,当x
<0,当x![]() (-3,2)时
(-3,2)时![]() >0 .
>0 .
(1)求![]() 在[0,1]内的值域.
在[0,1]内的值域.
(2)若ax2+bx+c≤0的解集为R,求实数c的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com