
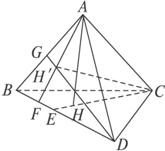
分析:要证H′是△ABD的重心,则只需证明AH′⊥BD,DH′⊥AB.由三垂线定理可知,只需证明BD⊥AC,AB⊥CD.由A在△BCD内的射影为△BCD的垂心易得上述两个垂直.
证明:从三角形垂心的定义知,连结CH并延长与BD交于E,则CE⊥BD.
∵AH⊥平面BDC,∴直线CA在平面BDC上的射影是直线CE.∴BD⊥AC.
从H′是C在平面ABD上的射影,知CH′⊥平面ABD,连结AH′并延长与BD交于F点,则直线AF是斜线CA在平面ABD的射影.∵BD⊥AC,
∴BD⊥AF.连结DH′并延长与AB交于G,同理从AB⊥CD可知AB⊥DG,所以H′是△ADB的垂心.
点评:本试题应注意两个问题:一是充分利用三角形垂心是三角形高的交点这一性质;二是三垂线定理及逆定理的反复利用,并且能顺利地找到平面的垂线,斜线在平面内的射影.


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:
 如右图所示,已知△OAB中,点C是以A为中心的点B的对称点,D在OB上,且
如右图所示,已知△OAB中,点C是以A为中心的点B的对称点,D在OB上,且| OD |
| DB |
| OA |
| a |
| OB |
| b |
| a |
| b |
| OC |
| DC |
| OE |
| OA |
查看答案和解析>>
科目:高中数学 来源: 题型:
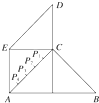 某县位于山区,居民的居住区域大致呈如右图所示的五边形,近似由一个正方形和两个等腰直角三角形组成,若AB=60km,AE=CD=30km,为了解决当地人民看电视难的问题,准备建一个电视转播台,理想方案是转播台距五边形各顶点的距离平方和最小,图中P1、P2、P3、P4是AC的五等分点,则转播台应建在( )
某县位于山区,居民的居住区域大致呈如右图所示的五边形,近似由一个正方形和两个等腰直角三角形组成,若AB=60km,AE=CD=30km,为了解决当地人民看电视难的问题,准备建一个电视转播台,理想方案是转播台距五边形各顶点的距离平方和最小,图中P1、P2、P3、P4是AC的五等分点,则转播台应建在( )查看答案和解析>>
科目:高中数学 来源: 题型:
某县位于山区,居民的居住区域大致呈如右图所示的五边形,近似由一个正方形和两个等腰直角三角形组成,若AB=60km,AE=CD=30km,为了解决当地人民看电视难的问题,准备建一个电视转播台,理想方案是转播台距五边形各顶点的距离平方和最小,图中P1、P2、P3、P4是AC的五等分点,则转播台应建在( )
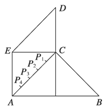
A.P1处 B.P2处
C.P3处 D.P4处
查看答案和解析>>
科目:高中数学 来源: 题型:
如右图所示,正方形ABCD,ABEF的边长都是1,并且平面ABCD⊥平面ABEF,点M在AC上移动,点N在BF上移动.若|CM|=|BN|=a(0<a<![]() ).
).
(1)求MN的长度;
(2)当a为何值时,MN的长度最短?
查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖南省高二上学期质量检测数学理卷 题型:选择题
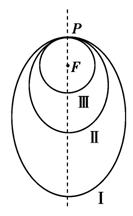
如右图所示,“嫦娥一号”探月卫星沿地月转移轨道飞向月球,在月
球附近一点P变轨进入以月球球心F为一个焦点的椭圆轨道Ⅰ绕月飞
行,之后卫星在P点第二次变轨进入仍以F为一个焦点的椭圆轨道Ⅱ
绕月飞行,最终卫星在P点第三次变轨进入以F为圆心的圆形轨道Ⅲ
绕月飞行,若用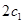 和
和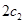 分别表示椭轨道Ⅰ和Ⅱ的焦距,用
分别表示椭轨道Ⅰ和Ⅱ的焦距,用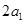 和
和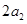
分别表示椭圆轨道Ⅰ和Ⅱ的长轴的长,给出下列式子:
①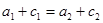 ②
②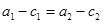 ③
③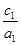 <
<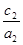 ④
④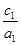 >
>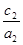 .
.
其中正确式子的序号是 ( )
(A)①③ (B)②③ (C)①④ (D)②④
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com