练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知点G是△ABC的重心.

    (1)求++；

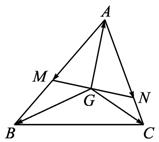
    (2)过G作直线与AB、AC两条边分别交于M、N，且=x·，=y·，试求的值.

    解：(1)方法1：延长AG到E，使得AG=GE，并设AE与BC交于D，则D是BC的中点.

    由BC和GE互相平分知四边形BGCE为平行四边形，∴+=.

    ∵+=0，∴++=0.

    方法2：延长AG与BC交于D，则=2=(+)+(+)，

    ∴++=+=0.

    (2)令=b，=c，则=xb，=yc，=13(b+c).

    ∴=-=(-x)b+c，=-=-b+(y-)c.

        由与共线，知(-x)(y-)=×(-)，从而=3.

    说明：本题第(1)小题采用了向量加法的平行四边形法则，也可以设三角形三个顶点坐标，利用教科书5.5节例2结论证明；第(2)小题还可利用5.3节例5结论求解：=(b+c)=(·+·)=·+·，由M、G、N共线得=1，

        即=3.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知点G是△ABC的重心，A（0，-1），B（0，1）．在x轴上有一点M，满足|
    MA
    |=|
    MC
    |    ，
    GM
    =λ
    AB
    (λ∈R)    （若△ABC的顶点坐标为A（x1，y1），B（x2，y2），C（x3，y3），则该三角形的重心坐标为G(
    x1+x2+x3
    3
    ，
    y1+y2+y3
    3
    )    ）．
    （1）求点C的轨迹E的方程．
    （2）设（1）中曲线E的左、右焦点分别为F1、F2，过点F2的直线l交曲线E于P、Q两点，求△F1PQ面积的最大值，并求出取最大值时直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知点G是△ABC的重心，
    AG
    =λ
    AB
    +μ
    AC
    (λ，μ∈R)    ，那么λ+μ=
     
    ；若∠A=120°，
    AB
    •
    AC
    =-2    ，则|
    AG
    |    的最小值是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知点G是△ABC的重心，点P是△GBC内一点，若
    AP
    =λ
    AB
    +μ
    AC
    ，则λ+μ    的取值范围是（　　）
    A、(
    1
    2
    ，1)
    B、(
    2
    3
    ，1)
    C、(1，
    3
    2
    )
    D、（1，2）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （文）已知奇函数f（x）满足f（x+3）=f（x），当x∈（0，1）时，函数f（x）=3x-1，则f(log
    1
    3
    36)    =
     

    （理）已知点G是△ABC的重心，O是空间任意一点，若
    OA
    +
    OB
    +
    OC
    =λ
    OG
    ，则λ的值是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    给出下列六个命题：
    ①sin1＜3sin
    1
    3
    ＜5sin
    1
    5

    ②若f'（x0）=0，则函数y=f（x）在x=x0取得极值；
    ③“?x0∈R，使得ex0＜0”的否定是：“?x∈R，均有ex≥0”；
    ④已知点G是△ABC的重心，过G作直线与AB，AC两边分别交于M，N两点，且
    AM
    =x
    AB
    ，
    AN
    =y
    AC
    ，则
    1
    x
    +
    1
    y
    =3    ；
    ⑤已知a=
    ∫
    π
    0
    sinxdx，    点(
    		3
    ，a)    到直线
    		3
    x-y+1=0    的距离为1；
    ⑥若|x+3|+|x-1|≤a2-3a，对任意的实数x恒成立，则实数a≤-1，或a≥4；
    其中真命题是
    ①③④⑤
    ①③④⑤
    （把你认为真命题序号都填在横线上）

    查看答案和解析>>

    同步练习册答案