
分析:由于B点在直线x=-1上移动,A点在x正半轴上移动,因此分类讨论应分两组进行:首先由B点在x轴上(即重合于D点)与不在x轴上讨论求函数的轨迹方程;第二组由圆锥曲线的定义对a>0的定义域进行讨论.
解:(1)当B点落在x轴上的D点时,∠AOB=π,∠AOB的平分线为y轴,y轴与AB的交点为原点,此时点C的轨迹为坐标原点O(0,0).
(2)当B点在x轴的上方时,设C(x,y),其中y>0,0<x<a,设B(-1,yB),yB>0,
∵Rt△ACE∽Rt△ABD,∴![]() =
=![]() .
.
∵a-x≠0,∴yB=![]() .
.
由l1到l2的角得
tan∠AOC=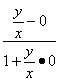 =
=![]() ,
,
tan∠COB=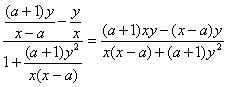 .
.
由tan∠AOC=tan∠COB得
![]() =
=![]() .
.
∵y>0,两边同除以y,得
(1-a)x2+(a+1)y2=2ax(0<x<a,y>0).
(3)当B点在x轴下方时,同理可求得C点的轨迹方程为(1-a)x2+(1+a)y2=2ax(0≤x<a,y<0).
由(1)(2)(3)得C点的轨迹方程为
(1-a)x2+(1+a)y2=2ax(0≤x<a). (*)
方程(*)是一个含有参数a的二元二次方程且不含xy项,表示何种曲线类型由x2和y2的系数确定.
(i)当a=1时,(*)化为y2=x(0≤x<1),为一段抛物线;(ii)当a≠1时,(*)化简为
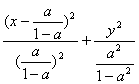 =1(0≤x<a).
=1(0≤x<a).
①当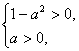 即0<a<1时,轨迹为椭圆位于0≤x<a之间的部分.
即0<a<1时,轨迹为椭圆位于0≤x<a之间的部分.
②当![]() 即a>1时,轨迹为双曲线在0≤x<a之间的一段.
即a>1时,轨迹为双曲线在0≤x<a之间的一段.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:
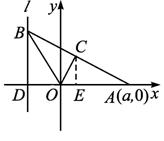
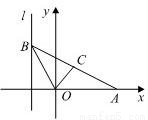
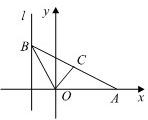 如图,给出定点A(a,0)(a>0,a≠1)和直线l:x=-1,B是直线l上的动点,∠BOA的角平分线交AB于点C.求点C的轨迹方程,并讨论方程表示的曲线类型与a值的关系.
如图,给出定点A(a,0)(a>0,a≠1)和直线l:x=-1,B是直线l上的动点,∠BOA的角平分线交AB于点C.求点C的轨迹方程,并讨论方程表示的曲线类型与a值的关系.查看答案和解析>>
科目:高中数学 来源:中学教材标准学案 数学 高二上册 题型:044
如图,给出定点A(a,0)(a>0)和直线l:x=-1,B是直线l上的一动点,∠BOA的平分线交AB于点C,求点C的轨迹方程,并讨论方程表示的曲线类型与a值的关系.(注:文科题设还有条件a≠1).
查看答案和解析>>
科目:高中数学 来源: 题型:
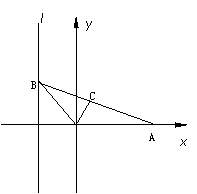
如图,给出定点A(![]() , 0) (
, 0) (![]() >0)和直线: x = 1 . B是直线l上的动点,ÐBOA的角平分线交AB于点C. 求点C的轨迹方程,并讨论方程表示的曲线类型与
>0)和直线: x = 1 . B是直线l上的动点,ÐBOA的角平分线交AB于点C. 求点C的轨迹方程,并讨论方程表示的曲线类型与![]() 值的关系.(14分)
值的关系.(14分)
 |
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,给出定点A(a,0) (a>0,a≠1)和直线l:x=-1,B是直线l上的动点,∠BOA的角平分线交AB于点C,求点C的轨迹方程,并讨论方程表示的曲线类型与a值的关系.

查看答案和解析>>
科目:高中数学 来源:1999年全国统一高考数学试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com