

如图,圆柱的轴截面ABCD是正方形,点E在底面的圆周上,AF⊥DE,F是垂足.
(1)求证:AF⊥DB;
(2)如果圆柱与三棱锥D-ABE的体积的比等于3π,求直线DE与平面ABCD所成的角.
| (1)证明:根据圆柱性质,DA⊥平面ABE.
∵EB ∴DA⊥EB. ∵AB是圆柱底面的直径,点E在圆周上, ∴AE⊥EB,又AE∩AD=A, 故得EB⊥平面DAE. ∵AF ∴EB⊥AF. 又AF⊥DE,且EB∩DE=E, 故得AF⊥平面DEB. ∵DB ∴AF⊥DB. (2) 解:过点E作EH⊥AB,H是垂足,连结DH.根据圆柱性质,平面ABCD⊥平面ABE,AB是交线.且EH
又DH ∠EDH是DE与平面ABCD所成的角. 设圆柱的底面半径为R,则DA=AB=2R,于是 V圆柱=2πR 3,
由V圆柱:VD-ABE=3π,得EH=R,可知H是圆柱底面的圆心,AH=R, DH= ∴∠EDH=arcctan
|


科目:高中数学 来源: 题型:
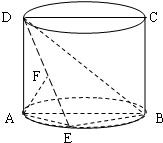 如图,圆柱的轴截面ABCD是正方形,点E在底面圆周上,点F在DE上,且AF⊥DE,若圆柱的侧面积与△ABE的面积之比等于4π.
如图,圆柱的轴截面ABCD是正方形,点E在底面圆周上,点F在DE上,且AF⊥DE,若圆柱的侧面积与△ABE的面积之比等于4π. 查看答案和解析>>
科目:高中数学 来源: 题型:
如图,圆柱的轴截面ABCD是正方形,点E在底面圆周上,点F在DE上,且AF⊥DE,若圆柱的侧面积与△ABE的面积之比等于4π。
(Ⅰ)求证:AF⊥BD;
(Ⅱ)求二面角A―BD―E的正弦值。

查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)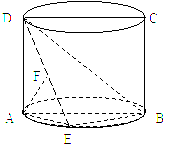 如图,圆柱的轴截面ABCD是正方形,点E在底面圆周上,点F在DE上,且AF⊥DE,若圆柱的侧面积与△ABE的面积之比等于4π.
如图,圆柱的轴截面ABCD是正方形,点E在底面圆周上,点F在DE上,且AF⊥DE,若圆柱的侧面积与△ABE的面积之比等于4π.
(Ⅰ)求证:AF⊥BD;(Ⅱ)求二面角A―BD―E的正弦值.
查看答案和解析>>
科目:高中数学 来源:2010年湖南省长沙市浏阳一中高考数学模拟试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2010年浏阳一中高考仿真模拟考试(理) 题型:解答题
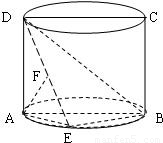
 如图,圆柱的轴截面ABCD是正方形,点E在底面圆周上,点F在DE上,且AF⊥DE,若圆柱的侧面积与△ABE的面积之比等于4π. 007
如图,圆柱的轴截面ABCD是正方形,点E在底面圆周上,点F在DE上,且AF⊥DE,若圆柱的侧面积与△ABE的面积之比等于4π. 007
(Ⅰ)求证:AF⊥BD;
(Ⅱ)求二面角A―BD―E的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com