
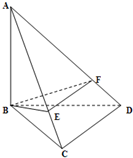
如图,在△BCD中,∠BCD=90°,BC=CD=1,AC⊥平面BCD,∠ADC=45°,E是线段AD的中点,F是线段AC上的一个动点.

(1)确定点F的位置,使平面ABD⊥平面BEF;
(2)当平面ABD⊥平面BEF时,求直线DB与EF所成的角.
解法一:(1)由已知可得AB=AD=BD=![]() .又AE=ED,则BE⊥AD.
.又AE=ED,则BE⊥AD.
由平面ABD⊥平面BEF得AD⊥平面BEF,
故AD⊥EF,即F应为过点E的AD的垂线和AC的交点.
由AC=CD知点F即为点C.
(2)由(1)知EF和BD所成的角即为EC与BD所成的角,
延长AC至G,使得CG=AC,连DG,则∠BDG即为CE与BD所成的角,
在△BDG中,BD=DG=BG,所以∠BDG=60°,即直线EF与直线BD所成的角为60°.
解法二:如图建立空间直角坐标系,则C(0,0,0),
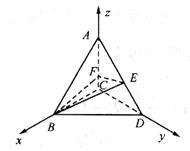
B(1,0,0),D(0,1,0),A(0,0,1),E(0,![]() ,
,![]() )
)
设F(0,0,![]() ),则
),则![]() =(0,一
=(0,一![]() ,
,![]() ,一
,一![]() ),
),
又![]() =(-1,
=(-1,![]() ,
,![]() ).
).
设n=(![]() ,
,![]() ,
,![]() )是平面BEF的一个法向量,
)是平面BEF的一个法向量,
则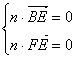 ,即
,即![]()
令![]() =1,则n=(2
=1,则n=(2![]() ,4
,4![]() 一1,1).
一1,1).
又m=(1,1,1)是平面ABD的一个法向量,要使平面ABD⊥平面BEF.
当且仅当m⊥n,即m?n=0,解得![]() =0.
=0.
∴F(0,0,0),即为点C.
(2)![]() ,
,![]() .
.
∴![]() <
<![]() >=
>=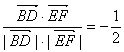 .
.
∴直线EF与直线BD所成的角为60°.


 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:
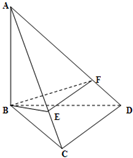 如图,在△BCD中,∠BCD=90°,AB⊥平面BCD,E、F分别是AC、AD上的动点,且
如图,在△BCD中,∠BCD=90°,AB⊥平面BCD,E、F分别是AC、AD上的动点,且| AE |
| AC |
| AF |
| AD |
查看答案和解析>>
科目:高中数学 来源: 题型:
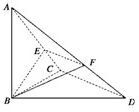 如图,在△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且
如图,在△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且| AE |
| AC |
| AF |
| AD |
查看答案和解析>>
科目:高中数学 来源:2014届河北省高一上学期二调数学 题型:解答题
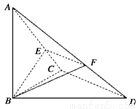
如图,在△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且==λ(0<λ<1).
(1)判断EF与平面ABC的位置关系并给予证明;
(2)是否存在λ,使得平面BEF⊥平面ACD,如果存在,求出λ的值,如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
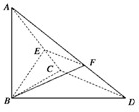 如图,在△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且
如图,在△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且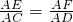 =λ(0<λ<1).
=λ(0<λ<1).查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| AE |
| AC |
| AF |
| AD |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com