练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在中，a,b,c是内角，A，B，C的对边，且.

    （I）求角B的大小；

    （II）若，求b的最小值.

    解（I）原式可化为

    （II）

    由余弦定理，得

    即b的最小值是1（此时△ABC为边长是1的等边三角形）

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    16、在正方体ABCD-A′B′C′D′中，过对角线BD′的一个平面交AA′于E，交CC′于F，则
    ①四边形BFD′E一定是平行四边形；
    ②四边形BFD′E有可能是正方形；
    ③四边形BFD′E在底面ABCD内的投影一定是正方形；
    ④平面BFD′E有可能垂直于平面BB′D．
    以上结论正确的为
    ①③④
    ．（写出所有正确结论的编号）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在正方体ABCD—A′B′C′D′中,过对角线BD′的一个平面交AA′于E,交CC′于F,则下列命题中真命题的个数是(    )

    ①BE∥D′F  ②四边形BFD′E有可能是正方形  ③四边形BFD′E在底面ABCD内的投影一定是正方形

    A.0                 B.1               C.2                 D.3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

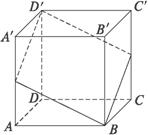
    在正方体ABCD—A′B′C′D′中，过对角线BD′的一个平面交AA′于E，交CC′于F，则

    ①四边形BFD′E一定是平行四边形；

    ②四边形BFD′E有可能是正方形；

    ③四边形BFD′E在底面ABCD内的投影一定是正方形；

    ④四边形BFD′E有可能垂直于平面BB′D

    以上结论正确的为________.（写出所有正确结论的编号）

    查看答案和解析>>

    科目：高中数学 来源：2014届浙江省高三上学期入学摸底文科数学试卷（解析版） 题型：填空题

    以下四个命题：①在△ABC中,内角A,B,C的对边分别为a,b,c,且，则；②设是两个非零向量且，则存在实数λ，使得；③方程在实数范围内的解有且仅有一个；④且，则；其中正确的是               

     

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年浙江省十校联合体高三上学期期初联考文科数学试卷（解析版） 题型：选择题

    四个命题

    （1） 在△ABC中,内角A,B,C的对边分别为a,b,c,且，则

    （2）设是两个非零向量且，则存在实数λ，使得；

    （3）方程在实数范围内的解有且仅有一个；

    （4）；

     其中正确的个数有（    ）

    A.1个    B.  2个    C. 3      D.4个

     

    查看答案和解析>>

    同步练习册答案