
(1)求证:平面PBD上平面PAC;
(2)求点A到平面PBD的距离;
(3)求二面角B-PC-A的大小.
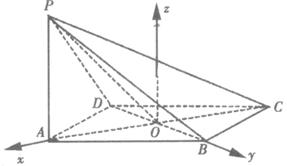
解法一:如图所示,以O为原点建立空间直角坐标系.

(1)平面PAC即xOz平面的一个法向量为n=(0,1,0);设平面PBD的一个法向量为n1=(1,y1,z1),
由n1⊥![]() ,n1⊥
,n1⊥![]() ,可得n1=(1,0,
,可得n1=(1,0,![]() )
)
由n·n1=(0,1,0)·(1,0,![]() )=0,得n⊥n1,
)=0,得n⊥n1,
所以平面PBD⊥平面PAC
(2) ![]() =(
=(![]() ,0,0),点A到平面PBD的距离
,0,0),点A到平面PBD的距离
d=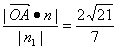
(3)平面PAC的一个法向量为(0,1,0),设平面PBC的一个法向量n2=(1,y2,z2)
由n2⊥![]() ,n2⊥
,n2⊥![]() 可得n2=(1,
可得n2=(1,![]() ,
,![]() )
)
∴cos<n,n2>=![]() ,
,
∴故所求的二面角为arecos![]() .
.
解法二:(1)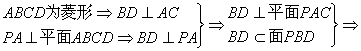 平面PBD⊥平面PAC
平面PBD⊥平面PAC
(2)连结PO,过点A作AE⊥PO,平面PAC∩平面PBD=PO,
∴AE⊥平面PBD,AE就是所求的距离,计算得AE=![]()
(3)过点O作OF⊥PC,连接BF,∵OF⊥平面PAC,由三垂线定理PC⊥BF,∴∠OFB为二面角B-PC-A的平面角,
经计算,AC=2![]() ,PC=4,OC=
,PC=4,OC=![]()
∵Rt△OFC∽Rt△PAC,
∴![]()
∴tan∠OFB=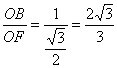
∴∠OFB=arctan![]()
即二面角B-PC-A的大小为arctan![]() .
.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:
 如图,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,∠BAD=60°.
如图,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,∠BAD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:
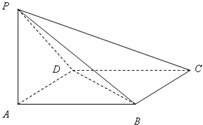 如图,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,∠BAD=60°.
如图,ABCD是菱形,PA⊥平面ABCD,PA=AD=2,∠BAD=60°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com