【答案】
分析:(1)对f(x)进行求导,根据曲线y=f(x)在点(1,f(1))处的切线与x轴平行,可以得f′(1)=0,代入求得k值,再利用导数研究函数的单调性;
(2)把已知的f(x)的解析式代入不等式f(x)≥(1+a)x-e
xlnx+b,将问题转化为h(x)=e
x-(a+1)x-b≥0,恒成立即可,对h(x)进行求导,对a+1与1的大小进行讨论求解;
解答:解:(1)∵函数f(x)=(k
2-klnx)e
x,
∴f′(x)=(k
2-klnx-
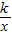
)e
x,
由题意知f′(1)=0,解得k=1或k=0(舍去)
所以f(x)=(1-lnx)e
x,f(x)=(1-lnx-
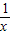
)e
x,
设g(x)=1-lnx-
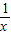
,则g(x)=-
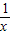
+
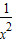
=
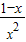
于是g(x)在区间(0,1)内为增函数,在(1,+∞)内为减函数,
所以g(x)在x=1处取得极大值,且g(1)=0;
所以g(x)≤0,故f'(x)≤0所以f(x)在(0,+∞)上是减函数.----(4分)
(Ⅱ) f(x)≥(1+a)x-e
xlnx+b?h(x)=e
x-(a+1)x-b≥0--(6分)
得h'(x)=e
x-(a+1)
①当a+1<1时,h'(x)>0⇒y=h(x)在x∈R上单调递增,
∴h(x)>h(0)=1-b≥0,所以0<b≤1.
此时(a+1)b<1.----(7分)
②当a+1=1时,h′(x)>0⇒y=h(x)在R上单调递增,
h(x)>h(0)=1-b≥0,可得b≤1,此时(a+1)b最大值为1;
③当a+1>1时,h′(x)>0?x>ln(a+1),h′(x)<0,
?x<ln(a+1),
所以当x=ln(a+1)时,h(x)
min=(a+1)-(a+1)ln(a+1)-b≥0
(a+1)b≤(a+1)
2-(a+1)
2 ln(a+1)(a+1>1)
令a+1=t,t>1
设F(t)=t
2-t
2lnt(t>1)
则F′(t)=t(1-2lnt)
F′(t)>0,?1<t<
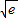
,F′(t)<0
?t>e,
当t=e时,F(t)
max=
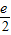
,
综上当
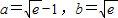
时,(a+1)b的最大值为
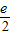
---(12分)
点评:此题考查利用导数研究函数的单调性,解题过程中用到了分类讨论和转化的思想,是一道综合性比较强的题,解答过程中要认真仔细的进行计算;

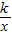 )ex,
)ex,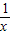 )ex,
)ex,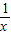 ,则g(x)=-
,则g(x)=-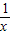 +
+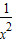 =
=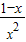
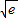 ,F′(t)<0
,F′(t)<0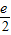 ,
,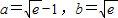 时,(a+1)b的最大值为
时,(a+1)b的最大值为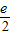 ---(12分)
---(12分)
