练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．若集合A={x|1≤2x≤8}，B={x|（x-2）（x+1）＞0}，则A∩B=（　　）
    A．（2，3]B．[2，3]C．（-∞，0）∪（0，2]D．（-∞，-1）∪（0，3]

    分析 解不等式求出集合A、B，根据交集的定义写出A∩B．

    解答 解：集合A={x|1≤2x≤8}={x|0≤x≤3}，
    B={x|（x-2）（x+1）＞0}={x|x＜-1或x＞2}，
    则A∩B={x|2＜x≤3}=（2，3]．
    故选：A．

    点评 本题考查了解不等式与交集的运算问题，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    8．已知函数f（x）=lnx-$\frac{1}{x}$，g（x）=ax+b．
    （1）若a=2，F（x）=f（x）-g（x），求F（x）的单调区间；
    （2）若函数g（x）=ax+b是函数f（x）=lnx-$\frac{1}{x}$图象的切线，求a+b的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．设Sn为等差数列{an}的前n项和，若$\frac{{S}_{1}}{{S}_{4}}$=$\frac{1}{10}$，则$\frac{{S}_{3}}{{S}_{5}}$=（　　）
    A．$\frac{2}{5}$B．$\frac{3}{5}$C．$\frac{3}{7}$D．$\frac{4}{7}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．函数f（x）=3sin（2x-$\frac{π}{3}$）的图象可以由y=3sin2x的图象（　　）
    A．向右平移$\frac{π}{3}$个单位长度得到B．向左平移$\frac{π}{3}$个单位长度得到
    C．向右平移$\frac{π}{6}$个单位长度得到D．向左平移$\frac{π}{6}$个单位长度得到

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

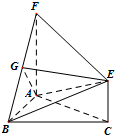    13．如图，三角形ABC和梯形ACEF所在的平面互相垂直，AB⊥BC，AF⊥AC，AF${\;}_{=}^{∥}$2CE，G是线段BF上一点，AB=AF=BC
    （Ⅰ）若EG∥平面ABC，求$\frac{BG}{BF}$的值；
    （Ⅱ）是否在线段BF上存在点G满足BF⊥平面AEG？请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．下面四个命题中的真命题是（　　）
    A．命题“?x≥2，均有x2-3x+2≥0”的否定是：“?x＜2，使得x2-3x+2＜0”
    B．命题“若x2=1，则x=1”的否命题为“若x2=1，则x≠1”
    C．采用系统抽样法从某班按学号抽取5名同学参加活动，学号为5、16、27、38、49的同学均被选出，则该班人数可能为60
    D．在某项测量中，测量结果X服从正态分布N（1，σ2）（σ＞0），若X在（0，1）内取值的概率为0.3，则X在（0，2）内取值的概率为0.6

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．私家车的尾气排放是造成雾霾天气的重要因素之一，因此在生活中我们应该提倡低碳生活，少开私家车，尽量选择绿色出行方式，为预防雾霾出一份力．为此，很多城市实施了机动车尾号限行，我市某报社为了解市区公众对“车辆限行”的态度，随机抽查了50人，将调查情况进行整理后制成如表：
    年龄（岁）[15，25）[25，35）[35，45）[45，55）[55，65）[65，75]
    频数510151055
    赞成人数469634
    （Ⅰ）完成被调查人员的频率分布直方图；
    （Ⅱ）若从年龄在[55，65），的被调查者中各随机选取2人进行追踪调查，记选中的2人中赞成“车辆限行”的人数为X，求随机变量X的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

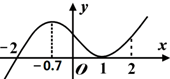
    15．已知函数f（x）的导函数f′（x）的图象如图所示，那么下面说法正确的是（　　）
    A．y=f（x）在（-∞，-0.7）上单调递增B．y=f（x）在（-2，2）上单调递增
    C．在x=1时，函数y=f（x）取得极值D．y=f（x）在x=0处切线的斜率小于零．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．已知$f（x）=\left\{\begin{array}{l}-2，0＜x＜1\\ 1，x≥1\end{array}\right.$，则不等式${log_2}x-（{{{log}_{\frac{1}{4}}}4x-1}）f（{{{log}_3}x+1}）≤5$的解集为（$\frac{1}{3}$，4]．

    查看答案和解析>>

    同步练习册答案