Question

求过点A（-1，2）且平行于向量a=（3，2）的直线方程.

Answer 1

思路分析：利用向量法来解决几何问题时，要将线段看成向量并用端点坐标来表示.

解法一：直线与a=（3，2）平行，

∴直线斜率k=.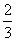

∴直线方程为y-2=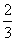(x+1),即2x-3y+8=0.

解法二：过点A且平行于向量的直线是唯一确定的，把这条直线记为l，在l上任取一点P（x,y），则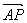∥a.

    如果点P不与点A重合，由向量平行，它们的坐标满足的条件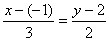,整理，得方程为2x-3y+8=0.

解法三：设P(x,y)为所求直线上任意一点，由题意知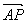∥a，

而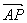=（x+1,y-2）,a=(3,2),

∴(x+1)·2-(y-2)·3=0,

化简得2x-3y+8=0，即为所求直线的方程.