
设函数![]() ,且
,且![]() ,其中n=1,2,3,….
,其中n=1,2,3,….
(I)计算a2,a3,a4的值;
(II)猜想数列{an}的通项公式,并用数字归纳法加以证明.
考点:
数学归纳法;数列递推式.
专题:
证明题;等差数列与等比数列;点列、递归数列与数学归纳法.
分析:
(I)由an+1=![]() ,a1=
,a1=![]() ,即可求得a2,a3,a4的值;
,即可求得a2,a3,a4的值;
(II)由a1,a2,a3,a4,可猜想an=![]() ,用数学归纳法证明,①当n=1时,去证明结论成立;②假设当n=k(k∈N*)时等式成立,去证明当n=k+1时,猜想也成立即可.
,用数学归纳法证明,①当n=1时,去证明结论成立;②假设当n=k(k∈N*)时等式成立,去证明当n=k+1时,猜想也成立即可.
解答:
解:(I)由题意,得an+1=![]() ,(1分)
,(1分)
因为a1=![]() ,
,
所以a2=![]() ,a3=
,a3=![]() ,a4=
,a4=![]() .(3分)
.(3分)
(II)解:由a1,a2,a3,a4,猜想an=![]() (5分)
(5分)
以下用数字归纳法证明:对任何的n∈N*,an=![]()
证明:①当n=1时,由已知,左边=![]() ,右边=
,右边=![]() =
=![]() ,所以等式成立.(7分)
,所以等式成立.(7分)
②假设当n=k(k∈N*)时等式成立,即ak=![]() ,(8分)
,(8分)
则n=k+1时,ak+1=![]() =
=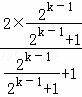 =
=![]() =
=![]() =
=![]() .
.
所以当n=k+1时,猜想也成立.(12分)
根据①和②,可知猜想对于任何n∈N*都成立.(13分)
点评:
本题考查数列递推式,考查数学归纳法,证明时用好归纳假设是关键,突出考查推理与证明的能力,属于中档题.


科目:高中数学 来源:2011-2012学年山东省高三第三次月考理科数学试卷 题型:解答题
已知定义在实数集上的函数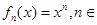 N
N ,其导函数记为
,其导函数记为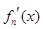 ,且满足
,且满足 ,其中
,其中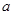 、
、 、
、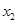 为常数,
为常数,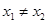 .设函数
.设函数
 R且
R且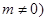 .
.
(Ⅰ)求实数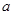 的值;
的值;
(Ⅱ)若函数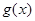 无极值点,其导函数
无极值点,其导函数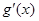 有零点,求m的值;
有零点,求m的值;
(Ⅲ)求函数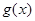 在
在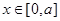 的图象上任一点处的切线斜率k的最大值
的图象上任一点处的切线斜率k的最大值
查看答案和解析>>
科目:高中数学 来源:2012-2013学年北京市西城区(北区)高二(下)期末数学试卷(理科)(解析版) 题型:解答题
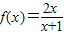 ,且
,且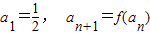 ,其中n=1,2,3,….
,其中n=1,2,3,….查看答案和解析>>
科目:高中数学 来源:2012-2013学年北京市西城区(北区)高二(下)期末数学试卷(文科)(解析版) 题型:解答题
 ,且
,且 ,其中n=1,2,3,….
,其中n=1,2,3,…. .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com