练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    从直线L：y＝x－2上一点P向圆C：x2＋y2＋2x－4y＝0引切线，则切线长的最小值为________．

    答案：
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：中学教材标准学案　数学　高二上册 题型：044

    设a＞0，如图，已知直线l：y＝ax及曲线C：y＝x2，C上的Q1的横坐标为a1(0＜a1＜a)．从C上的点Qn(n≥1)作直线平行于x轴，交直线l于点Pn+1，再从点Pn+1作直线平行于y轴，交曲线C于点Qn+1．Qn(n＝1，2，3，…)的横坐标构成数列{an}．

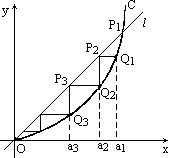
    (Ⅰ)试求an+1与an的关系，并求{an}的通项公式；

    (Ⅱ)当a＝1，a1≤时，证明：；

    (Ⅲ)当a＝1时，证明：

    查看答案和解析>>

    科目：高中数学 来源：教材完全解读　高中数学　必修5(人教B版课标版) 人教B版课标版 题型：038

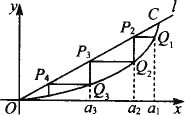
    设a＞0，如图，已知直线l：y＝ax及曲线C：y＝x2，C上的点Q1的横坐标为a1(0＜a1＜a)，从C上的点Qn(n≥1)作直线平行于x轴，交直线l于点Pn+1作直线平行于y轴，交曲线C于点Qn+1，Qn(n＝1，2，3，…)的横坐标构成数列{an}．试求an+1与an的关系，并求{an}的通项公式．

    查看答案和解析>>

    科目：高中数学 来源：潮阳一中2007届高三摸底考试理科数学 题型：044

    已知焦点在x轴上的双曲线C的两条渐近线过坐标原点，且两条渐近线与以点A(0，)为圆心，1为半径为圆相切，又知C的一个焦点与A关于直线y＝x对称．

    (1)求双曲线C的方程；

    (2)若Q是双曲线C上的任一点，F1、F2为双曲线C的左、右两个焦点，从F1引∠F1QF2的平分线的垂线，垂足为N，试求点N的轨迹方程．

    (3)设直线y＝mx＋1与双曲线C的左支交于A、B两点，另一直线L经过M(－2，0)及AB的中点，求直线L在y轴上的截距b的取值范围．S

    查看答案和解析>>

    科目：高中数学 来源：黑龙江省哈三中2011－2012学年高一上学期期中考试数学试题 题型：013

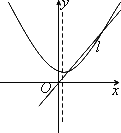
    当函数的自变量取值区间与值域区间相同时，我们称这样的区间为该函数的保值区间．函数的保值区间有(－∞，m]、[m，n]、[n，＋∞)三种形式．以下四个图中：虚线为二次函数图像的对称轴，直线l的方程为y＝x，从图象可知，下列四个二次函数中有2个保值区间的函数是

    [　　]
    A．

    B．

    C．

    D．

    查看答案和解析>>

    同步练习册答案