Question

如图,已知正三棱柱ABC—A₁B₁C₁,D是AC的中点,∠C₁DC=60°.

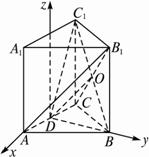
(1)求证:AB₁∥平面BC₁D;

(2)求二面角D-BC₁-C的大小.?

Answer 1

解析：以AC的中点D为原点建立坐标系,如图,设|AD|=1,??

?

∵∠C₁DC=60°,?

∴|CC₁|=.?

则A(1,0,0),B(0, ,0),C(-1,0,0),A₁(1,0,),B₁(0,,),C₁(-1,0,).?

(1)连结B₁C交BC₁于O,则O是B₁C的中点,连结DO,则O(-, ,).?

=(-1,,),=(- ,,).?

则.?

∵AB₁平面BC₁D,?

∴AB₁∥平面BC₁D.?

(2) =(-1,0,), =(1,,-).?

设平面BC₁D的法向量为n=(x,y,z),

则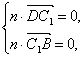

即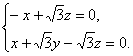则有y=0.令z=1.?

则n=(,0,1).?

设平面BCC₁B₁的法向量为m=(x′,y′,z′),?

=(0,0,), =(1,,-),?

?

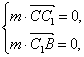即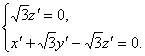

∴z′=0.?

令y=-1,解得m=(,-1,0).?

二面角DBC₁C的余弦值为cos〈n,m〉=.?

∴二面角D-BC₁-C的大小为arccos.