
 .
.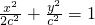 (c>0),
(c>0), ,又C(1,0),
,又C(1,0), ,
,
 ,
, ;
; ,
,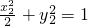 ,
, ,
, ?
? ,
, ,
, ,化简得:9m2-8<0,
,化简得:9m2-8<0, )(3m-2
)(3m-2 )<0,
)<0, .
. b,则b2=c2,a2=2c2设出椭圆的标准方程,设出已知直线与E的交点A与B的坐标,然后把直线方程代入到设出的椭圆方程中,消去y得到关于x的一元二次方程,利用韦达定理得到两个之和和两根之积的关系式,同时利用求出C的坐标,和设出的A和B的坐标,由
b,则b2=c2,a2=2c2设出椭圆的标准方程,设出已知直线与E的交点A与B的坐标,然后把直线方程代入到设出的椭圆方程中,消去y得到关于x的一元二次方程,利用韦达定理得到两个之和和两根之积的关系式,同时利用求出C的坐标,和设出的A和B的坐标,由 得到A与B横坐标之间的关系式,三者联立即可求出A与B的横坐标及c的值,把c的值代入所设的椭圆方程即可得到椭圆E的方程;
得到A与B横坐标之间的关系式,三者联立即可求出A与B的横坐标及c的值,把c的值代入所设的椭圆方程即可得到椭圆E的方程;

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:单选题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 +
+ =
= +
+ ,三棱锥P-ABC中D位AB上任一点,h为过点P的三棱锥的高,三棱锥P-ADC、P-BDC、P-ABC的内切球的半径分别为r1,r2,r,请类比平面三角形中的结论,写出类似的一个恒等式为________.
,三棱锥P-ABC中D位AB上任一点,h为过点P的三棱锥的高,三棱锥P-ADC、P-BDC、P-ABC的内切球的半径分别为r1,r2,r,请类比平面三角形中的结论,写出类似的一个恒等式为________.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 ,下底AB=3,按平行于上、下底边取x轴,则直观图A′B′C′D′的面积为 ________.
,下底AB=3,按平行于上、下底边取x轴,则直观图A′B′C′D′的面积为 ________.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com