练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    用二分法求函数的一个正零点(精确到0.1)．

    答案：略
    解析：

    由于f(0)=－3＜0，f(2)=3＞0，可取区间[0，2]作为计算的初始区间．

    用二分法逐次计算，列表如下：

    ∵区间[1.6875，1.751]的长度小于0.1，

    ∴可取这个区间的中点作为所求函数的一个正零点的近似值．


    提示：

    ①用二分法求函数的近似零点，合理确定初始区间是关键．②二分法的缺点是刻板，机械，有时要进行大量的重复计算．优点是一种通法，只要按部就班地去做，总会算出结果，另一优点是它可以让计算机来实现，可编写程序，快速地求出一个函数的零点．③如果某一计算方法对某一类问题(不是个别问题)都有效，计算可以一步一步地进行，每一步都能得到唯一的结果，我们常把这一类问题的求解过程叫做解决这一类问题的一种算法．二分法就是求图象连续不间断的函数的变号零点的一种算法．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    用二分法求函数的一个正零点（误差不超过）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    用二分法求函数的一个零点，其参考数据如下：

    f(1.6000)=0.200

    f(1.5875)=0.133

    f(1.5750)=0.067

    f(1.5625)=0.003

    f(1.5562)=-0.029

    f(1.5500)=-0.060

    据此数据，可得方程的一个近似解（精确到0.01）为     ▲   

    查看答案和解析>>

    科目：高中数学 来源：2015届辽宁省五校协作体高一上学期联合竞赛数学试卷（解析版） 题型：选择题

    用“二分法”求函数的一个正实数零点，其参考数据如下：

     

     

     

     

    那么方程的一个近似根（精确到0.1）为  (    )           

      A. 1.2                 B. 1.3                C. 1.4              D. 1.5

     

    查看答案和解析>>

    科目：高中数学 来源：黑龙江省哈尔滨市2010届高三一模数学（理）试题 题型：选择题

    用二分法求函数的一个零点，根据参考数据，可得函数的一个零点的近似解（精确到）为（    ）（参考数据：）

    （A）             （B）             （C）  2.6        （D）

     

    查看答案和解析>>

    科目：高中数学 来源：2010年江苏省高一第三阶段检测数学卷 题型：填空题

    用二分法求函数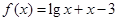的一个零点，其参考数据如下：

    f(2)≈-0.699

    f(3) ≈0.477

    f(2.5) ≈-0.102

    f(2.75) ≈0.189

    f(2.625) ≈0.044

    f(2.5625)≈-0.029

    f(2.59375)≈0.008

    f(2.57813≈-0.011

    根据此数据，可得方程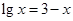的一个近似解（精确到0.1）为     

     

    查看答案和解析>>

    同步练习册答案