
| A. | 25 | B. | 12 | C. | $\frac{25}{2}$ | D. | 9 |
分析 直线ax+by-2=0(a,b∈R*)平分圆x2+y2-6x-4y-12=0,可得:直线ax+by-2=0(a,b∈R*)经过圆心,于是a+b=1.再利用“乘1法”与基本不等式的性质即可得出.
解答 解:圆x2+y2-6x-4y-12=0化为(x-3)2+(y-2)2=25,圆心为C(3,2),
∵直线ax+by-2=0(a,b∈R*)平分圆x2+y2-6x-4y-12=0,
∴直线ax+by-2=0(a,b∈R*)经过圆心C(3,2),
∴3a+2b-2=0,化为$\frac{3}{2}$a+b=1.
∴$\frac{3}{a}$+$\frac{2}{b}$=($\frac{3}{2}$a+b)($\frac{3}{a}$+$\frac{2}{b}$)=$\frac{13}{2}$+$\frac{3a}{b}$+$\frac{3b}{a}$≥$\frac{13}{2}$+2$\sqrt{\frac{3a}{b}•\frac{3b}{a}}$=$\frac{25}{2}$,
当且仅当a=b=$\frac{2}{5}$时取等号.
∴$\frac{3}{a}$+$\frac{2}{b}$的最小值是$\frac{25}{2}$.
故选:C.
点评 本题考查了圆的性质、“乘1法”与基本不等式的性质,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{1}{4}$,-$\frac{1}{6}$) | B. | (-$\frac{1}{2}$,-$\frac{1}{4}$] | C. | (-$\frac{1}{6}$,0] | D. | (-$\frac{1}{2}$,-$\frac{1}{6}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\sqrt{{x}^{2}}$ | B. | y=$\frac{{x}^{2}}{x}$ | ||
| C. | y=($\sqrt{x}$)2 | D. | y=logaax(a>0且a≠1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 2 | C. | -2或1 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
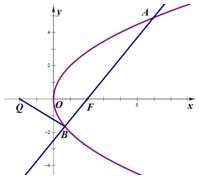 已知抛物线E:y2=2px(p>0)的准线是圆C:(x-1)2+y2=4的切线.
已知抛物线E:y2=2px(p>0)的准线是圆C:(x-1)2+y2=4的切线.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 数学成绩好 | 数学成绩一般 | 总计 | |
| 物理成绩好 | |||
| 物理成绩一般 | |||
| 总计 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com