
 ,E、F分别为CD、AB中点,沿EF将梯形AFED折起,使得∠AFB=60°,点G为FB的中点.
,E、F分别为CD、AB中点,沿EF将梯形AFED折起,使得∠AFB=60°,点G为FB的中点.
解:(1)∵AF=BF且∠AFB=60°,
∴△ABF是等边三角形
又∵G是FB的中点,
∴AG⊥BF
∵翻折前的等腰梯形ABCD中,E、F分别是CD、AB的中点,
∴EF⊥AB,可得翻折后EF⊥AF,EF⊥BF
∵AF、BF是平面ABF内的相交直线,
∴EF⊥平面ABF
∵AG 平面ABF,
平面ABF,
∴AG⊥EF,
∵BF、EF是平面BCEF内的相交直线,
∴AG⊥平面BCEF
(2)取EC中点M,连接MC、MD、MG
∵AF∥DE,AF 平面ABF,DE
平面ABF,DE 平面ABF,
平面ABF,
∴DE∥平面ABF,
同理可得:CE∥平面ABF,
∵DE、CE是平面DCE内的相交直线,
∴平面DCE∥平面ABF,可得AG∥DM
∵AG⊥平面BCEF,∴DM⊥平面BCEF,
∵MG 平面BCEF,∴DM⊥MG,
平面BCEF,∴DM⊥MG,
∵梯形BFEC中,EC=FG=BG=1,BF∥EC,
∴四边形EFGC是平行四边形,可得EF∥CG
∵EF⊥平面ABF,
∴CG⊥平面ABF,可得CG⊥BG
Rt△BCG中,BG=1,BC= ,可得CG=
,可得CG= =1
=1
∴Rt△GCM中,GM= =
=
又∵DM= CE=
CE= ,
,
∴Rt△GDM中,DG= =
=



科目:高中数学 来源: 题型:
 如图,在等腰梯形ABCD中,AB∥DC,AB=4,CD=2,等腰梯形的高为3,O为AB中点,PO⊥平面ABCD,垂足为O,PO=2,EA∥PO.
如图,在等腰梯形ABCD中,AB∥DC,AB=4,CD=2,等腰梯形的高为3,O为AB中点,PO⊥平面ABCD,垂足为O,PO=2,EA∥PO.查看答案和解析>>
科目:高中数学 来源: 题型:
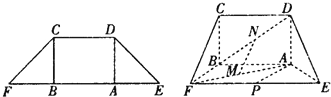 如图,在等腰梯形CDEF中,CB、DA是梯形的高,AE=BF=2,AB=2
如图,在等腰梯形CDEF中,CB、DA是梯形的高,AE=BF=2,AB=2| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 选修4-1;几何证明选讲.
选修4-1;几何证明选讲.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•河北模拟)如图,在等腰梯形ABCD中,CD=2,AB=4,AD=BC=
(2012•河北模拟)如图,在等腰梯形ABCD中,CD=2,AB=4,AD=BC=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com