练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    (文)一个多面体的直观图及三视图如图所示：(其中M、N分别是AF、BC的中点)．

    (Ⅰ)求证：MN∥平面CDEF；

    (Ⅱ)求多面体A－CDEF的体积．

    答案：
    解析：

    　　解：由三视图可知，该多面体是底面为直角三角形的直三棱住ADE－BCF，　　2分

    　　且AB＝BC＝BF＝2，DE＝CF＝2

    　　∴∠CBF＝　　4分

    　　(Ⅰ)取BF中点G，连MG、NG，由M、N分别为AF、BC的中点可得，NG∥CF，MG∥EF，　　6分

    　　∴平面MNG∥平面CDEF．

    　　∴MN∥平面CDEF．　　8分

    　　(Ⅱ)取DE的中点H．

    　　∵AD＝AE，∴AH⊥DE，在直三棱柱ADE－BCF中，平面ADE⊥平面CDEF，面ADE∩面CDEF＝DE．

    　　∴AH⊥平面CDEF．　　10分

    　　∴多面体A－CDEF是以AH为高，以矩形CDEF为底面的棱锥，在△ADE中，AH＝，

    　　∴棱锥A－CDEF的体积为　　12分


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

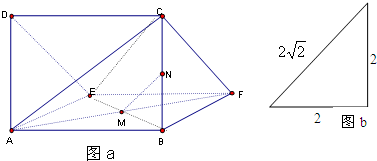    如图，一个多面体的直观图如图a所示，它的正视图和俯视图都是边长为2的正方形，左视图如图b所示．已知M、N分别是AF、BC的中点．
    （1）求证：MN∥平面CDEF；
    （2）求四棱锥E-ABCD的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    一个多面体的直观图和三视图如图所示，其中M、G分别是AB、DF的中点．
    （1）在AD上（含A、D端点）确定一点P，使得GP∥平面FMC；
    （2）一只苍蝇在几何体ADF-BCE内自由飞翔，求它飞入几何体F-AMCD内的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2007•上海模拟）一个多面体的直观图，前视图（正前方观察），俯视图（正上方观察），侧视图（左侧正前方观察）如图所示．
    （1）求A1A与平面ABCD所成角的大小及面AA1D1与面ABCD所成二面角的大小；
    （2）求此多面体的表面积和体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （08年德州市质检文）（12分）一个多面体的直观图及三视图如图所示（其中M、N分别是AF、BC的中点）

       （1）求证：MN//平面CDEF；

       （2）求多面体A―CDEF的体积.

     

    查看答案和解析>>

    同步练习册答案