
设y=f(x)为区间[0,1]上的连续函数,且恒有0≤f(x) ≤1,可以用随机模拟方法近似计算积分![]() ,先产生两组(每组N个)区间[0,1]上的均匀随机数
,先产生两组(每组N个)区间[0,1]上的均匀随机数![]() ,
,![]() …,
…,![]() 和
和![]() ,
,![]() …,
…,![]() ,由此得到N个点(
,由此得到N个点(![]() ,
,![]() )(i=1,2,…,N),再数出其中满足
)(i=1,2,…,N),再数出其中满足![]() ((i=1,2,…,N))的点数
((i=1,2,…,N))的点数![]() ,那么由随机模拟方法可得积分
,那么由随机模拟方法可得积分![]() 的近似值为 .
的近似值为 .
科目:高中数学 来源: 题型:
| π |
| 4 |
| x |
| 2 |
| π |
| 2 |
| 2π |
| 3 |
| π |
| 6 |
| 2π |
| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 4 |
| x |
| 2 |
| π |
| 2 |
| 2π |
| 3 |
| π |
| 6 |
| 2π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
设y=f(x)为区间[0,1]上的连续函数,且恒有0≤f(x) ≤1,可以用随机模拟方法近似计算积分![]() ,先产生两组(每组N个)区间[0,1]上的均匀随机数
,先产生两组(每组N个)区间[0,1]上的均匀随机数![]() ,
,![]() …,
…,![]() 和
和![]() ,
,![]() …,
…,![]() ,由此得到N个点(
,由此得到N个点(![]() ,
,![]() )(i=1,2,…,N),在数出其中满足
)(i=1,2,…,N),在数出其中满足![]() ≤
≤![]() ((i=1,2,…,N))的点数
((i=1,2,…,N))的点数![]() ,那么由随机模拟方法可得积分
,那么由随机模拟方法可得积分![]() 的近似值为 .
的近似值为 .
查看答案和解析>>
科目:高中数学 来源:2010年高考试题(海南卷)解析版(理) 题型:填空题
设y=f(x)为区间[0,1]上的连续函数,且恒有0≤f(x) ≤1,可以用随机模拟方法近似计算积分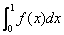 ,先产生两组(每组N个)区间[0,1]上的均匀随机数
,先产生两组(每组N个)区间[0,1]上的均匀随机数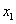 ,
,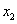 …,
…,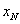 和
和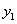 ,
,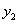 …,
…,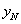 ,由此得到N个点(
,由此得到N个点(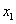 ,
,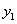 )(i=1,2,…,N),在数出其中满足
)(i=1,2,…,N),在数出其中满足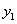 ≤
≤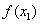 ((i=1,2,…,N))的点数
((i=1,2,…,N))的点数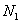 ,那么由随机模拟方法可得积分
,那么由随机模拟方法可得积分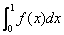 的近似值为
.
的近似值为
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com