练习册

  • 练习册
  • 试题
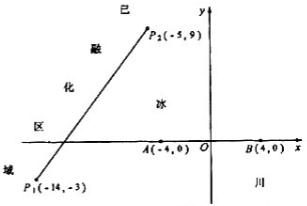    精英家教网 > 高中数学 > 题目详情
    如图2-2所示，在△ABC中,=c,=a,=b,且a·b=b·c=c·a，试判断△ABC的形状.

    图2-2

    解：∵a·b=b·c,∴b·(a-c)=0.

    又b=-(a+c),

    ∴-(a+c)·(a-c)=0,即c2-a2=0.

    ∴|c|=|a|.同理,|b|=|a|,

    故|a|=|b|=|c|,所以△ABC为等边三角形.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    精英家教网为了考察冰川的融化状况，一支科考队在某冰川山上相距8Km的A、B两点各建一个考察基地，视冰川面为平面形，以过A、B两点的直线为x轴，线段AB的垂直平分线为y轴建立平面直角坐标系（如图）．考察范围到A、B两点的距离之和不超过10Km的区域．
    （1）求考察区域边界曲线的方程：
    （2）如图所示，设线段P1P2（3）是冰川的部分边界线（不考虑其他边界），当冰川融化时，边界线沿与其垂直的方向朝考察区域平行移动，第一年移动0.2km，以后每年移动的距离为前一年的2倍．问：经过多长时间，点A恰好在冰川边界线上？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

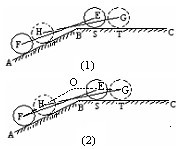    （2013•徐汇区一模）某种型号汽车四个轮胎半径相同，均为R=40cm，同侧前后两轮胎之间的距离（指轮胎中心之间距离）为l=280cm （假定四个轮胎中心构成一个矩形）．当该型号汽车开上一段上坡路ABC（如图（1）所示，其中∠ABC=a（
    3
    4
    π＜a＜π    ），且前轮E已在BC段上时，后轮中心在F位置；若前轮中心到达G处时，后轮中心在H处（假定该汽车能顺利驶上该上坡路）．设前轮中心在E和G处时与地面的接触点分别为S和T，且BS=60cm，ST=100cm．（其它因素忽略不计）
    （1）如图（2）所示，FH和GE的延长线交于点O，求证：OE=40cot
    α
    2
    +60    （cm）；
    （2）当a=
    5
    6
    π时，后轮中心从F处移动到H处实际移动了多少厘米？（精确到1cm）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在一条直线型的工艺流水线上有3个工作台，将工艺流水线用如图2-19所示的数轴表示，各工作台的坐标分别为x1，x2，x3，每个工作台上有若干名工人．现要在x1与x3之间修建一个零件供应站，使得各工作台上的所有工人到供应站的距离之和最短．
    （1）若每个工作台上只有一名工人，试确定供应站的位置；
    （2）设从左到右工作台上的工人人数依次为2，1，3，试确定供应站的位置，并求所有工人到供应站的距离之和的最小值．精英家教网

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    为了了解中学生的体能情况,抽取了某校一个年级的部分学生进行一次跳绳次数测试,将所得的数据整理后,画出频率分布直方图,如图2-2所示,已知图中从左到右前三个小组的频率分别为0.1,0.3,0.4,第一小组的频数为5.

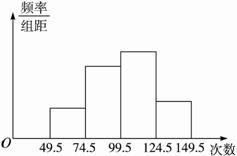
                          图2-2

    (1)求第四小组的频率；

    (2)参加这次测试的学生数是多少？

    (3)若次数在75次以上(含75次)为达标,试估计该年级学生跳绳测试的达标率是多少？

    (4)这次测试中,学生跳绳的次数的中位数落在四个小组中的哪个小组内？说明理由.

    查看答案和解析>>

    同步练习册答案