
若数列{an}为等差数列,ap=q,aq=p(p≠q),则ap+q为
p+q
0
-(p+q)
![]()
|
法一:∵ap=a1+(p-1)d,aq=a1+(q-1)d, ∴ 两式相减得(p-q)d=q-p. ∵p≠q, ∴d=-1. 代入得a1=p+q-1. ∴ap+q=a1+(p+q-1)d=p+q-1+(p+q-1)(-1)=0. ∴应选B. 法二:∵ap=aq+(p-q)d, ∴q=p+(p-q)d. ∵p≠q,∴d=-1. ∴ap+q=ap+(p+q-p)d=q+q(-1)=0. ∴应选B. 法三:不防设p<q,由于等差数列中,an关于n的图象是一条直线上均匀排开的一群孤立的点,故三点(p,ap),(q,aq),(p+q,ap+q)共线.设ap+q=m,由已知得三点(p,q),(q,p),(p+q,m)共线(如图).
由△ABE∽△BCF,得 ∴ ∴ ∴m=0. ∴应选B. |


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:高中数学 来源: 题型:
| an+2-an+1 | an+1-an |
查看答案和解析>>
科目:高中数学 来源: 题型:
| an+2-an+1 |
| an+1-an |
| 2n-1 |
| an+1 |
查看答案和解析>>
科目:高中数学 来源:学习周报 数学 北师大课标高二版(必修5) 2009-2010学年 第4期 总第160期 北师大课标版(必修5) 题型:013
在数列
{an}中,n∈N+,若①③
②④
①④
②③④
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 时,
时,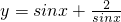 的最小值是
的最小值是 .
.查看答案和解析>>
科目:高中数学 来源:2011年上海市黄浦区高考数学一模试卷(文理合卷)(解析版) 题型:解答题
 =p(p为常数),则称数列{an}为“等差比”数列,p叫数列{an}的“公差比”.现给出如下命题:
=p(p为常数),则称数列{an}为“等差比”数列,p叫数列{an}的“公差比”.现给出如下命题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com