练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知平面上任意两点A(x1，y1)，B(x2，y2)，求这两点连线的斜率，画出算法框图，并用算法语句描述．

    答案：
    解析：

    　　分析：对于平面上给定的两点A(x1，y1)和B(x2，y2)，若x1＝x2，则直线AB的斜率不存在；若x1≠x2，则直线AB的斜率k＝．因此在输入两点的坐标后应先判断x1＝x2是否成立，若成立，应输出斜率不存在的信息；若不成立，可将的值赋予变量k后输出，故可利用条件语句实现这一算法．

    　　解：算法框图如图所示：

    　　算法语句描述如下：


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

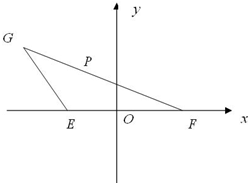    精英家教网已知E、F是x轴上的点，坐标原点O为线段EF的中点，G、P是坐标平面上的动点，点P在线段FG上，|
    .
    FG
    |    =10，|
    .
    EF
    |    =6，(
    .
    PE
    +
    1
    2
    .
    EG
    )•
    .
    EG
    =0
    （1）求P的轨迹C的方程；
    （2）A、B为轨迹C上任意两点，且
    .
    OE
    =α
    .
    OA
    +(1-α)
    .
    OB
    ，M为AB的中点，求△OEM面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知对任意平面向量
    AB
    =(x，y)    ，将
    AB
    绕其起点沿顺时针方向旋转θ角得到向量
    AP
    =(xcosθ+ysinθ，-xsinθ+ycosθ)    ，叫做将点B绕点A沿顺时针方向旋转θ角得到点P．
    （1）已知平面内点A（1，2），点B(1+
    		2
    ，2-2
    		2
    )    ，将点B绕点A沿顺时针方向旋转
    π
    4
    得到点P，求点P的坐标；
    （2）设平面内曲线3x2+3y2+2xy=4上的每一点绕坐标原点O沿顺时针方向旋转
    π
    4
    得到的点的轨迹是曲线C，求曲线C的方程；
    （3）过（2）中曲线C的焦点的直线l与曲线C交于不同的两点A、B，当
    OA
    •
    OB
    =0    时，求△AOB的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知平面内A、B、C、D四点，任意三点不在同一直线上，则连接任意两点的所有向量的个数为（　　）

    查看答案和解析>>

    科目：高中数学 来源：学习周报　数学　北师大课标高二版(选修1－2)　2009－2010学年　第31期　总第187期 北师大课标 题型：044

    已知平面上任意输入两点A(x1，y1)，B(x2，y2)，输出这两点连线的斜率，请画出算法框图．

    查看答案和解析>>

    同步练习册答案