
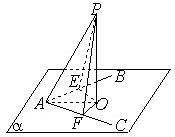
 如图,已知∠BAC在平面α内,P∉α,∠PAB=∠PAC,求证:点P在平面α上的射影在∠BAC的平分线上.
如图,已知∠BAC在平面α内,P∉α,∠PAB=∠PAC,求证:点P在平面α上的射影在∠BAC的平分线上.  证明:作PO⊥α,PE⊥AB,PF⊥AC,
证明:作PO⊥α,PE⊥AB,PF⊥AC,
|
|


 阶梯计算系列答案
阶梯计算系列答案科目:高中数学 来源: 题型:
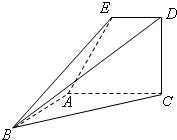 如图,已知直角梯形ACDE所在的平面垂直于平面ABC,∠BAC=∠ACD=90°,∠EAC=60°,AB=AC=AE.
如图,已知直角梯形ACDE所在的平面垂直于平面ABC,∠BAC=∠ACD=90°,∠EAC=60°,AB=AC=AE.查看答案和解析>>
科目:高中数学 来源: 题型:013
如图,已知∠BAC是二面角α-a-β的平面角,那么下列各结论中错误的是
[
]A
.BA是AC在α内的射影B
.AC是AB在β内的射影C
.a⊥平面ABCD
.AB⊥AC
查看答案和解析>>
科目:高中数学 来源:101网校同步练习 高一数学 苏教版(新课标·2004年初审) 苏教版 题型:047
如图,已知∠BAC在平面α内,P![]() α,∠PAB=∠PAC.求证:点P在平面α上的射影在∠BAC的平分线上.
α,∠PAB=∠PAC.求证:点P在平面α上的射影在∠BAC的平分线上.

查看答案和解析>>
科目:高中数学 来源:2009-2010学年数学暑假作业05(必修2)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com