
| AP |
| OA |
| OB |
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:
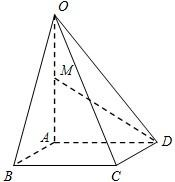 如图,在四棱锥O-ABCD中,底面ABCD是边长为1的菱形,∠ABC=
如图,在四棱锥O-ABCD中,底面ABCD是边长为1的菱形,∠ABC=| π | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
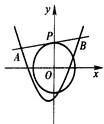 设点P(m,n)在圆x2+y2=2上,l是过点P的圆的切线,切线l与函数y=x2+x+k(k∈R)的图象交于A,B两点,点O是坐标原点.
设点P(m,n)在圆x2+y2=2上,l是过点P的圆的切线,切线l与函数y=x2+x+k(k∈R)的图象交于A,B两点,点O是坐标原点.查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省、金陵中学、南京外国语学校高三三校联考数学卷 题型:解答题
如图,在四棱锥O-ABCD中,底面ABCD是边长为1的菱形,∠ABC=45°,OA⊥底面ABCD,OA=2,M为OA的中点.

(1)求异面直线AB与MD所成角的大小;
(2)求平面OAB与平面OCD所成二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源:江苏同步题 题型:解答题
 ,OA⊥底面ABCD,OA=2,M为OA的中点.
,OA⊥底面ABCD,OA=2,M为OA的中点.
查看答案和解析>>
科目:高中数学 来源:2008-2009学年河北省衡水中学高一(下)第二次调研数学试卷(必修2)(解析版) 题型:解答题
 ,OA⊥底面ABCD,OA=2,M为OA的中点.
,OA⊥底面ABCD,OA=2,M为OA的中点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com