
如图的几何体中,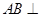 平面
平面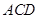 ,
,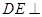 平面
平面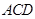 ,△
,△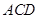 为等边三角形,
为等边三角形,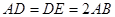 ,
,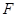 为
为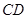 的中点.
的中点.
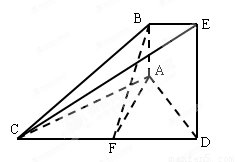
(1)求证: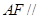 平面
平面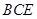 ;
;
(2)求证:平面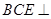 平面
平面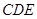 .
.
证明见解析.
【解析】
试题分析:(1)要证线面平行,关键是在平面内找一条与待证直线平行的直线,本题中,由于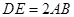 ,
,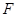 是中点,故很容易让人联想到取另一中点,这里我们取
是中点,故很容易让人联想到取另一中点,这里我们取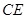 中点
中点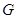 ,则
,则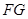 ∥
∥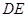 ∥
∥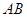 ,
,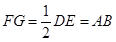 ,故
,故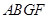 是平行四边形,从而有
是平行四边形,从而有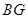 ∥
∥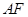 ,平行线找到了,结论得证;(2)要证面垂直,就是要证线面垂直,关键是找哪个平面内的直线,同样本题里由于
,平行线找到了,结论得证;(2)要证面垂直,就是要证线面垂直,关键是找哪个平面内的直线,同样本题里由于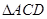 是等边三角形,故
是等边三角形,故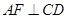 ,从而很快得到结论
,从而很快得到结论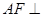 平面
平面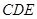 ,而(1)中有
,而(1)中有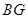 ∥
∥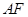 ,则有
,则有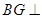 平面
平面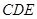 ,这就是我们要的平面的垂线,由此就证得了面面垂直.
,这就是我们要的平面的垂线,由此就证得了面面垂直.
试题解析:(1)证明:取 的中点
的中点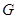 ,连结
,连结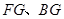 .
.
∵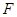 为
为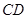 的中点,∴
的中点,∴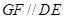 且
且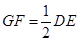 .
.
∵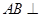 平面
平面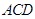 ,
,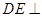 平面
平面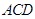 ,
,
∴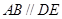 ,∴
,∴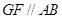 . 又
. 又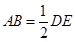 ,∴
,∴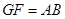 .
.
∴四边形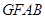 为平行四边形,则
为平行四边形,则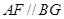 .
.
∵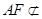 平面
平面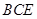 ,
,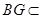 平面
平面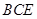 ,
∴
,
∴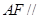 平面
平面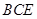 . 7分
. 7分
(2)证明:∵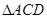 为等边三角形,
为等边三角形,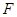 为
为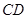 的中点,∴
的中点,∴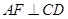
∵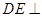 平面
平面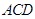 ,
,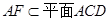 ,∴
,∴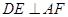 .
.
∵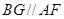 ,∴
,∴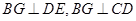 又
又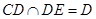 ,
,
∴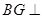 平面
平面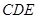 .
.
∵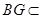 平面
平面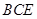 ,
∴平面
,
∴平面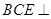 平面
平面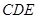 . 14分
. 14分
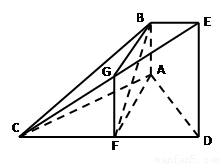
考点:(1)线面平行;(2)面面垂直.


科目:高中数学 来源: 题型:
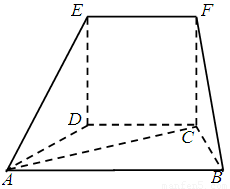
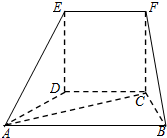 在如图的几何体中,平面CDEF为正方形,平面ABCD为等腰梯形,AB∥CD,AB=2BC,∠ABC=60°,AC⊥FB.
在如图的几何体中,平面CDEF为正方形,平面ABCD为等腰梯形,AB∥CD,AB=2BC,∠ABC=60°,AC⊥FB.查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省广州市高三年级调研测试理科数学试卷(解析版) 题型:解答题
在如图的几何体中,平面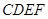 为正方形,平面
为正方形,平面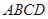 为等腰梯形,
为等腰梯形,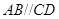 ,
,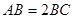 ,
,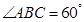 ,
,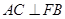 .
.
(1)求证: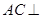 平面
平面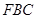 ;
;
(2)求直线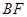 与平面
与平面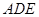 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省南京市高三下学期入学测试数学试卷 题型:解答题
(本小题满分14分)如图的几何体中, 平面
平面 ,
, 平面
平面 ,△
,△ 为等边三角形,
为等边三角形,
 ,
, 为
为 的中点.
的中点.

(1)求证: 平面
平面 ;
;
(2)求证:平面 平面
平面 .
.
查看答案和解析>>
科目:高中数学 来源:广东省惠州市2011-2012学年高三第一次调研考试文科数学 题型:解答题
(本小题满分14分)
如图的几何体中, 平面
平面 ,
, 平面
平面 ,△
,△ 为等边三角形
为等边三角形 ,
, 为
为 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求证:平面 平面
平面 。
。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com