练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知曲线 ，一条长为8的弦AB的两个端点在H上运动，弦AB的中点为M，求距y轴最近的点M的坐标.

    解析：曲线 为双曲线 的右支.　　这里 　　 ∴e＝2
    　　右准线l： 　设 　作
    　　则 　∴ 　∴ 　①
    　　又双曲线右焦点 由双曲线第二定义得　 　②
    　　∴②代入①得 ③当且仅当 ，即AB为焦点弦时等号成立.
    　　∴由③ 当且仅当弦AB通过焦点 时等号成立.
    　　注意到曲线H过焦点垂直于对称轴的弦长为6<8，故条件可以满足.　∴ 　　④
    　　此时， ， ，　而 ，
    　　于是有⑤　　因此由④⑤得，距y轴最近的点M的坐标为 .
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

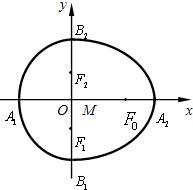    精英家教网已知半椭圆
    x2
    a2
    +
    y2
    b2
    =1(x≥0)    与半椭圆
    y2
    b2
    +
    x2
    c2
    =1(x≤0)    组成的曲线称为“果圆”，其中a2=b2+c2，a＞0，b＞c＞0．如图，设点F0，F1，F2是相应椭圆的焦点，A1，A2和B1，B2是“果圆”与x，y轴的交点，
    （1）若三角形F0F1F2是边长为1的等边三角形，求“果圆”的方程；
    （2）若|A1A|＞|B1B|，求
    b
    a
    的取值范围；
    （3）一条直线与果圆交于两点，两点的连线段称为果圆的弦．是否存在实数k，使得斜率为k的直线交果圆于两点，得到的弦的中点的轨迹方程落在某个椭圆上？若存在，求出所有k的值；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在A、B、C、D四小题中只能选做2题，每小题10分，共计20分，请在答题纸指定区域内作答，解答应写出文字说明、证明过程或演算步骤．
    A．选修4-1：（几何证明选讲）
    如图，从O外一点P作圆O的两条切线，切点分别为A，B，
    AB与OP交于点M，设CD为过点M且不过圆心O的一条弦，
    求证：O，C，P，D四点共圆．
    B．选修4-2：（矩阵与变换）
    已知二阶矩阵M有特征值λ=3及对应的一个特征向量e1=[
     
    1
    1
    ]，并且矩阵M对应的变换将点（-1，2）变换成（9，15），求矩阵M．
    C．选修4-4：（坐标系与参数方程）
    在极坐标系中，曲线C的极坐标方程为p=2
    		2
    sin（θ-
    π
    4
    ），以极点为原点，极轴为x轴的正半轴建立平面直角坐标系，直线l的参数方程为
    x=1+
    4
    5
    t
    y=-1-
    3
    5
    t
    （t为参数），求直线l被曲线C所截得的弦长．
    D．选修4-5（不等式选讲）
    已知实数x，y，z满足x+y+z=2，求2x2+3y2+z2的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

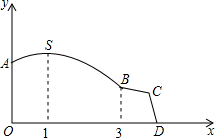    精英家教网安通驾校拟围着一座山修建一条环形训练道路OASBCD，道路的平面图如图所示（单位：km），已知曲线ASB为函数y=Asin（ωx+φ）（A＞0，0＜ω＜1，|φ|＜
    π
    2
    ），x∈[0，3]的图象，且最高点为S（1，2），折线段AOD为固定线路，其中AO=
    		3
    ，OD=4，折线段BCD为可变线路，但为保证驾驶安全，限定∠BCD=120°．
    （1）求A，ω，φ的值；
    （2）应如何设计，才能使折线段道路BCD最长？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    给出下列命题：

    ①过一点与已知曲线相切的直线有且只有一条；②函数的对称中心是；③对任意实数a,b则④取一根长为3m的绳子，拉直后在任意位置剪断，那么剪得两段的长度都不少于1m的概率是；⑤如果△A1B1C1的三个内角的余弦值分别等于△A2B2C2的三个内角的正弦值，则△A1B1C1为锐角三角形，△A2B2C2为钝角三角形.其中真命题的序号是             （将所有真命题的序号都填上）.      

    查看答案和解析>>

    同步练习册答案