
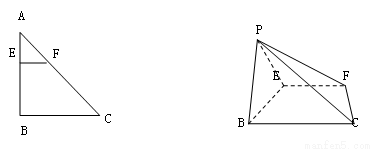
如图,在![]() 点
点![]() 上,过点
上,过点![]() 做
做![]() //
//![]() 将
将![]() 的位置(
的位置(![]() ),
),
使得![]() .
.
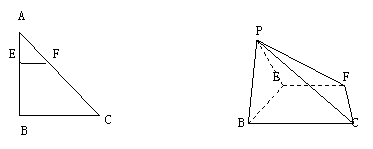

(1)求证:![]() . (2)试问:当点
. (2)试问:当点![]() 上移动时,二面角
上移动时,二面角![]() 的平面角的余弦值是否为定值?若是,求出定值,若不是,说明理由.
的平面角的余弦值是否为定值?若是,求出定值,若不是,说明理由.
解:(1)在![]() 中,
中,![]()
![]() 又
又![]() 平面PEB.
平面PEB.
又![]() 平面PEB,
平面PEB, ![]() ………………5分
………………5分
(2)解法一:过P作PQ![]() BE于点Q,垂足为Q;过Q作QH
BE于点Q,垂足为Q;过Q作QH![]() FC,垂足为H。则
FC,垂足为H。则![]() 即为所求二面角的平面角。……………………………………………………………8分
即为所求二面角的平面角。……………………………………………………………8分
设PE=x,则EQ=![]() ,PQ=
,PQ=![]() ,………………………………………………10分
,………………………………………………10分
QH=![]() ,…………………………………………………12分
,…………………………………………………12分
故![]() ,……………………………………………………13分
,……………………………………………………13分
![]() ,即二面角P-FC-B的平面角的余弦值为定值
,即二面角P-FC-B的平面角的余弦值为定值![]() ……14分
……14分
解法二:
在平面PEB内,经P点作PD![]() BE于D,由(1)知EF
BE于D,由(1)知EF![]() 面PEB,
面PEB,
![]() EF
EF![]() PD.
PD.![]() PD
PD![]() 面BCEF.在面PEB内过点B作直线BH//PD,则BH
面BCEF.在面PEB内过点B作直线BH//PD,则BH![]() 面BCFE.以B点为坐标原点,
面BCFE.以B点为坐标原点,![]() 的方向分别为x轴,y轴,z轴的正方向建立空间直角坐标系. ………………6分
的方向分别为x轴,y轴,z轴的正方向建立空间直角坐标系. ………………6分
设PE=x(0<x<4)又![]() [ http://wx.jtyjy.com/]
[ http://wx.jtyjy.com/]
在![]() 中,
中,![]()
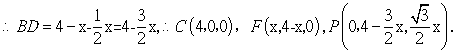
………………………………………………………………………………………8分
从而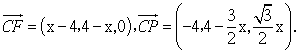
设![]() 是平面PCF的一个法向量,由
是平面PCF的一个法向量,由![]()
![]()
得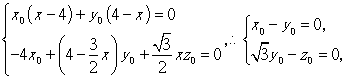 取
取![]() 得
得
![]() 是平面PFC的一个法向量. …………………………………11分
是平面PFC的一个法向量. …………………………………11分
又平面BCF的一个法向量为![]() ………………………………12分
………………………………12分
设二面角![]() 的平面角为
的平面角为![]() ,则
,则![]()
![]()
因此当点E在线段AB上移动时,二面角![]() 的平面角的余弦值为定值
的平面角的余弦值为定值![]() [ http://wx.jtyjy.
[ http://wx.jtyjy.
………………………………………………………………………………………14分


科目:高中数学 来源: 题型:
 (2011•盐城模拟)(本题文科学生做)如图,在平面直角坐标系xoy中,已知F1(-4,0),F2(4,0),A(0,8),直线y=t(0<t<8)与线段AF1、AF2分别交于点P、Q.
(2011•盐城模拟)(本题文科学生做)如图,在平面直角坐标系xoy中,已知F1(-4,0),F2(4,0),A(0,8),直线y=t(0<t<8)与线段AF1、AF2分别交于点P、Q.查看答案和解析>>
科目:高中数学 来源: 题型:
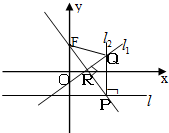 (2012•威海二模)如图,在平面直角坐标系xoy中,设点F(0,p)(p>0),直线l:y=-p,点p在直线l上移动,R是线段PF与x轴的交点,过R、P分别作直线l1、l2,使l1⊥PF,l2⊥l l1∩l2=Q.
(2012•威海二模)如图,在平面直角坐标系xoy中,设点F(0,p)(p>0),直线l:y=-p,点p在直线l上移动,R是线段PF与x轴的交点,过R、P分别作直线l1、l2,使l1⊥PF,l2⊥l l1∩l2=Q.查看答案和解析>>
科目:高中数学 来源:2012-2013学年河南省南阳市高三第八次周考理科数学试卷(解析版) 题型:解答题
(本小题满分12分)如图,在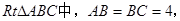 点
点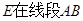 上,过点
上,过点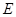 做
做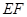 //
//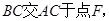 将
将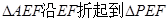 的位置(
的位置(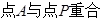 ),
),
使得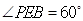 .
.
(I)求证: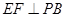 (II)试问:当点
(II)试问:当点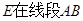 上移动时,二面角
上移动时,二面角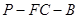 的平面角的余弦值是否为定值?若是,求出定值,若不是,说明理由.
的平面角的余弦值是否为定值?若是,求出定值,若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源:2014届江西省高二第二次月考理科数学试卷(解析版) 题型:解答题
(本小题14分) 如图,在平面直角坐标系xoy中,设点F(0, p)(p>0), 直线l : y= -p, 点P在直线l上移动,R是线段PF与x轴的交点, 过R、P分别作直线 、
、 ,使
,使 ,
,
 .
.
(1)求动点Q的轨迹C的方程;
(2)在直线l上任取一点M做曲线C的两条切线,设切点为A、B,求证:直线AB恒过一定点;
(3)对(2)求证:当直线MA, MF, MB的斜率存在时,直线MA, MF, MB的斜率的倒数成等差数列.
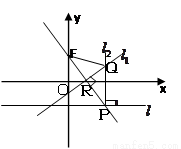
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com