
(1)![]() ;
;
(2)sinαcosα;
(3)3sin2α+2.
思路分析:若由tanα=3,求sinα,cosα的值,则要将α分一、三象限讨论,那么sinα,cosα的正负号就不确定了,所以解本题要注意应用基本关系式.对于(2)、(3)两题还应注意“1”的代换.
解:(1)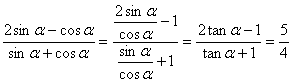 .
.
(2)∵![]() ,
,
又将tanα=3代入,得![]() .
.
(3)3sin2α+2=3sin2α+2(sin2α+cos2α)
=5sin2α+2cos2α=![]()
=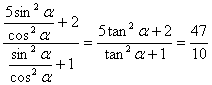 .
.
方法归纳 这类题的解法体现了化归思想的应用,即对只含有正弦、余弦的齐次式,可根据同角三角函数的商数关系,通过除以某一齐次项,转化成只含有正切的式子.这种化弦为切的技巧,有着广泛的应用.
深化升华 凡是分子、分母是某个角的正弦、余弦函数的齐次多项式,都可以用这个角的正切函数来表示.在三角知识中“1”的变换很多,除了平方关系之外,还有为了凑出某个公式的条件,也可以乘以“1”.


科目:高中数学 来源: 题型:
| π |
| 3 |
| π |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
| 2π |
| 3 |
| 5π |
| 6 |
| π |
| 3 |
| 3 |
| 5 |
| 4 |
| 5 |
查看答案和解析>>
科目:高中数学 来源:江西省新余一中2010届高三第六次模拟考试数学理科试题 题型:044
已知sin(2α+β)=3sinβ,设tanα=x,tanβ=y,记y=f(x).
(1)求f(x)的表达式;
(2)定义正数数列{an}:a1=![]() ,
,![]() =2an·f(an)(n∈N*).试求数列{an}的通项公式;
=2an·f(an)(n∈N*).试求数列{an}的通项公式;
(3)在(2)的条件下,记bn= ,设数列{bn}的前n项和为Rn.已知正实数λ满足:对任意正整数n,Rn≤λn恒成立,求λ的最小值.
,设数列{bn}的前n项和为Rn.已知正实数λ满足:对任意正整数n,Rn≤λn恒成立,求λ的最小值.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| π |
| 3 |
| π |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
| 2π |
| 3 |
| 5π |
| 6 |
| π |
| 3 |
| 3 |
| 5 |
| 4 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:

(1)指出动点P的轨迹(即说明动点P在满足给定的条件下运动时所形成的图形),证明你的结论;
(2)以轨迹上的动点P为顶点的三棱锥P-CDE的最大体积是正四棱锥S—ABCD体积的几分之几?
(3)设动点P在G点的位置时三棱锥P-CDE的体积取最大值V1,二面角G—DE—C的大小为α,二面角G—CE—D的大小为β,求tanα∶tanβ的值;
(4)若将“E是BC的中点”改为“E是BC上异于B、C的一定点”,其他条件不变,请指出点P的轨迹,证明你的结论.
查看答案和解析>>
科目:高中数学 来源:2008-2009学年江苏省南通市如皋市、海安县高一(上)期末数学试卷(解析版) 题型:解答题
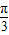 )(x∈R),且
)(x∈R),且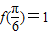 .
.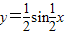 的图象;
的图象;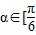 ,
,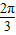 ,
,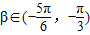 ,
,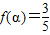 ,f(β)=-
,f(β)=- ,
,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com