
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD//BC,∠ADC=90°,
平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,
BC=![]() AD=1,CD=
AD=1,CD=![]() .
.
(Ⅰ)若点M是棱PC的中点,求证:PA // 平面BMQ;
(Ⅱ)求证:平面PQB⊥平面PAD;
(Ⅲ)若二面角M-BQ-C为30°,设PM=tMC,试确定t的值 .
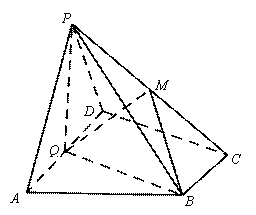
证明:(Ⅰ)连接AC,交BQ于N,连接MN. ……………………1分
∵BC∥AD且BC=![]() AD,即BC
AD,即BC![]() AQ.
AQ.
∴四边形BCQA为平行四边形,且N为AC中点,
又∵点M是棱PC的中点,
∴ MN // PA ……………………2分
∵ MN![]() 平面MQB,PA
平面MQB,PA![]() 平面MQB,…………………3分
平面MQB,…………………3分
∴ PA // 平面MBQ. ……………………4分
(Ⅱ)∵AD // BC,BC=![]() AD,Q为AD的中点,
AD,Q为AD的中点,
∴四边形BCDQ为平行四边形,∴CD // BQ . ……………………6分
∵∠ADC=90° ∴∠AQB=90° 即QB⊥AD.
又∵平面PAD⊥平面ABCD
且平面PAD∩平面ABCD=AD, ……………………7分
∴BQ⊥平面PAD. ……………………8分
∵BQ![]() 平面PQB,
平面PQB,
 ∴平面PQB⊥平面PAD. …………………9分
∴平面PQB⊥平面PAD. …………………9分
另证:AD // BC,BC=![]() AD,Q为AD的中点∴ BC // DQ 且BC= DQ,
AD,Q为AD的中点∴ BC // DQ 且BC= DQ,
∴ 四边形BCDQ为平行四边形,∴CD // BQ .
∵ ∠ADC=90° ∴∠AQB=90° 即QB⊥AD. …………………6分
∵ PA=PD, ∴PQ⊥AD. ……………………7分
∵ PQ∩BQ=Q,∴AD⊥平面PBQ. …………………8分
∵ AD![]() 平面PAD,
平面PAD,
∴平面PQB⊥平面PAD. ……………………9分
(Ⅲ)∵PA=PD,Q为AD的中点, ∴PQ⊥AD.
∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD, ∴PQ⊥平面ABCD.……………10分
(不证明PQ⊥平面ABCD直接建系扣1分)
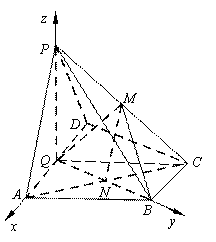
如图,以Q为原点建立空间直角坐标系.
则平面BQC的法向量为![]() ;
;
![]() ,
,![]() ,
,![]() ,
,![]() .………11分
.………11分
设![]() ,
,
则![]() ,
,![]() ,∵
,∵![]() ,
,
∴ 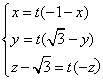 , ∴
, ∴ 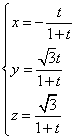 ……………………12分
……………………12分
在平面MBQ中,![]() ,
,![]() ,
,
∴ 平面MBQ法向量为![]() . ……………………13分
. ……………………13分
∵二面角M-BQ-C为30°, 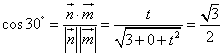 ,∴
,∴ ![]() .……14分
.……14分


科目:高中数学 来源: 题型:
 如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知AB=3,AD=2,PA=2,PD=2
如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知AB=3,AD=2,PA=2,PD=2| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=4,PA=3,点A在PD上的射影为点G,点E在AB上,平面PEC⊥平面PDC.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=4,PA=3,点A在PD上的射影为点G,点E在AB上,平面PEC⊥平面PDC.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,∠BCD=120°,BC⊥AB,CD⊥AD,BC=CD=PA=a,
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,∠BCD=120°,BC⊥AB,CD⊥AD,BC=CD=PA=a,查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在四棱锥P-ABCD中,底面是边长为a的菱形,∠ABC=60°PD⊥面ABCD,PC=a,E为PB中点
如图,在四棱锥P-ABCD中,底面是边长为a的菱形,∠ABC=60°PD⊥面ABCD,PC=a,E为PB中点查看答案和解析>>
科目:高中数学 来源: 题型:
 (2008•武汉模拟)如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,BC∥AD,且∠BAD=90°,又PA⊥底面ABCD,BC=AB=PA=1,AD=2.
(2008•武汉模拟)如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,BC∥AD,且∠BAD=90°,又PA⊥底面ABCD,BC=AB=PA=1,AD=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com