练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．某校设计了一个实验学科的实验考查方案：考生从6道备选题中一次性随机抽取3题，按照题目要求独立完成全部实验操作．规定：至少正确完成其中2题获得学分2分，便可通过考察．已知6道备选题中考生甲有4题能正确完成：考生乙每题正确完成的概率都是$\frac{2}{3}$，且每题正确完成与否互不影响．求：
    （Ⅰ）分别写出甲、乙两考生正确完成题数的概率分布列，并计算数学期望；
    （Ⅱ）请你判断两考生的实验操作学科能力，比较他们能通过本次考查的可能性大小．

    分析 （Ⅰ）由已知得甲正确完成题数X的可能取值为1，2，3，分别求出相应的概率，由此能求出甲考生正确完成题数X的概率分布列和数学期望；乙正确完成题数Y的可能取值为0，1，2，3，且Y～B（3，$\frac{2}{3}$），由此能求出乙考生正确完成题数Y的概率分布列和数学期望．
    （Ⅱ）E（X）=E（Y）=2，求出D（X）和D（Y），得到D（X）＜D（Y），再求出P（X≥2）和P（Y≥2），得到P（ξ≥2）＞P（η≥2），由此判断甲的实验操作能力强．

    解答 解：（Ⅰ）由已知得甲正确完成题数X的可能取值为1，2，3，
    P（X=1）=$\frac{{C}_{4}^{1}{C}_{2}^{2}}{{C}_{6}^{3}}$=$\frac{1}{5}$，
    P（X=2）=$\frac{{C}_{4}^{2}{C}_{2}^{1}}{{C}_{6}^{3}}$=$\frac{3}{5}$，
    P（X=3）=$\frac{{C}_{4}^{3}}{{C}_{6}^{3}}$=$\frac{1}{5}$，
    ∴甲考生正确完成题数X的概率分布列为：

     X 1 2 3
     P $\frac{1}{5}$ $\frac{3}{5}$ $\frac{1}{5}$
    EX=$1×\frac{1}{5}+2×\frac{3}{5}+3×\frac{1}{5}$=2．
    乙正确完成题数Y的可能取值为0，1，2，3，且Y～B（3，$\frac{2}{3}$），
    P（Y=0）=${C}_{3}^{0}（\frac{1}{3}）^{3}$=$\frac{1}{27}$，
    P（Y=1）=${C}_{3}^{1}（\frac{2}{3}）（\frac{1}{3}）^{2}$=$\frac{6}{27}$，
    P（Y=2）=${C}_{3}^{2}（\frac{2}{3}）^{2}（\frac{1}{3}）$=$\frac{12}{27}$，
    P（Y=3）=${C}_{3}^{3}（\frac{2}{3}）^{3}$=$\frac{8}{27}$，
    ∴甲考生正确完成题数Y的概率分布列为：
     Y 0 1 2 3
     P $\frac{1}{27}$ $\frac{6}{27}$ $\frac{12}{27}$ $\frac{8}{27}$
    E（Y）=$0×\frac{1}{27}+1×\frac{6}{27}+2×\frac{12}{27}+3×\frac{8}{27}$=2．
    （Ⅱ）∵E（X）=E（Y）=2，
    D（X）=（1-2）2×$\frac{1}{5}$+（2-2）2×$\frac{3}{5}$+（3-2）2×$\frac{1}{5}$=$\frac{2}{5}$，
    D（Y）=$3×\frac{2}{3}×\frac{1}{3}$=$\frac{2}{3}$，
    D（X）＜D（Y），
    ∵P（X≥2）=$\frac{3}{5}+\frac{1}{5}$=$\frac{4}{5}$，
    P（Y≥2）=$\frac{12}{27}+\frac{8}{27}$=$\frac{20}{27}$，
    ∴P（ξ≥2）＞P（η≥2）
    ①从做对题数的数学期望考查，两人水平相当；从做对题数的方差考查，甲较稳定；
    ②从至少完成2题的概率考查，甲获得通过的可能性大，
    因此，可以判断甲的实验操作能力强．

    点评 本题考查概率的求法，考查离散型随机变量的分布列和数学期望的求法，是中档题，解题时要认真审题，注意二项分布的性质的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    10．已知三棱锥P-ABC的各顶点都在同一球的面上，且PA⊥平面ABC，若球O的体积为$\frac{20\sqrt{5}π}{3}$（球的体积公式为$\frac{4π}{3}$R3，其中R为球的半径），AB=2，AC=1，∠BAC=60°，则三棱锥P-ABC的体积为（　　）
    A．$\frac{\sqrt{3}}{3}$B．$\frac{2\sqrt{3}}{3}$C．$\sqrt{3}$D．$\frac{4\sqrt{3}}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

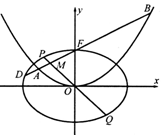    11．如图，在平面直角坐标系xOy中，椭圆C1：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的离心率为$\frac{{\sqrt{3}}}{2}$，抛物线C2：x2=4y的焦点F是C1的一个顶点．
    （I）求椭圆C1的方程；
    （II）过点F且斜率为k的直线l交椭圆C1于另一点D，交抛物线C2于A，B两点，线段DF的中点为M，直线OM交椭圆C1于P，Q两点，记直线OM的斜率为k'．
    （i）求证：k•k'=-$\frac{1}{4}$；
    （ii）△PDF的面积为S1，△QAB的面积为是S2，若S1•S2=λk2，求实数λ的最大值及取得最大值时直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．在平面直角坐标系xOy中，已知抛物线C：x2=4y，点P是C的准线l上的动点，过点P作C的两条切线，切点分别为A，B，则△AOB面积的最小值为（　　）
    A．$\sqrt{2}$B．2C．2$\sqrt{2}$D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．已知向量$\overrightarrow{m}$=（$\sqrt{3}$cosωx，cosωx），$\overrightarrow{n}$=（sinωx，cosωx）（ω＞0），函数f（x）=$\overrightarrow{m}$•$\overrightarrow{n}$的最小正周期为π．
    （Ⅰ）求ω的值及函数f（x）的单调递增区间；
    （Ⅱ）在钝角△ABC中，角A，B，C所对的边分别为a，b，c，已知a=1，b=$\sqrt{3}$，当f（A）取得最大值时，求边c．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知A、F分别是椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左顶点、右焦点，点P为椭圆C上一动点，当PF⊥x轴时，AF=2PF．
    （1）求椭圆C的离心率；
    （2）若椭圆C存在点Q，使得四边形AOPQ是平行四边形（点P在第一象限），求直线AP与OQ的斜率之积；
    （3）记圆O：x2+y2=$\frac{ab}{{a}^{2}+{b}^{2}}$为椭圆C的“关联圆”．若b=$\sqrt{3}$，过点P作椭圆C的“关联圆”的两条切线，切点为M、N，直线MN的横、纵截距分别为m、n，求证：$\frac{3}{{m}^{2}}$+$\frac{4}{{n}^{2}}$为定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知函数f（x）=$\frac{t{x}^{2}-1}{x}$-（t+1）lnx，t∈R，其中t∈R．
    （1）若t=1，求证：x＞1，f（x）＞0成立；
    （2）若t≥1，且f（x）＞1在区间[$\frac{1}{e}$，e]上恒成立，求t的取值范围；
    （3）若t＞$\frac{1}{e}$，判断函数g（x）=x[f（x）+t+1]的零点的个数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．为加快新能源汽车产业发展，推进节能减排，国家对消费者购买新能源汽车给予补贴，其中对纯电动乘用车补贴标准如表：
    新能源汽车补贴标准
    车辆类型续驶里程R（公里）
    100≤R＜180180≤R＜280＜280
    纯电动乘用车2.5万元/辆4万元/辆6万元/辆
    某校研究性学习小组，从汽车市场上随机选取了M辆纯电动乘用车，根据其续驶里程R（单次充电后能行驶的最大里程）作出了频率与频数的统计表：
    分组频数频率
    100≤R＜18030.3
    180≤R＜2806x
    R≥280yz
    合计M1
    （1）求x、y、z、M的值；
    （2）若从这M辆纯电动乘用车任选3辆，求选到的3辆车续驶里程都不低于180公里的概率；
    （3）如果以频率作为概率，若某家庭在某汽车销售公司购买了2辆纯电动乘用车，设该家庭获得的补贴为X（单位：万元），求X的分布列和数学期望值E（X）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．设i是虚数单位，若复数$a+\frac{2i}{1-i}$（a∈R）是纯虚数，则a=（　　）
    A．-1B．1C．-2D．2

    查看答案和解析>>

    同步练习册答案