
求证:在钝角△ABC中,若C为钝角,则tanAtanB<1.
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:高中数学 来源: 题型:
证明:假设___________,则∠B是直角或钝角.
(1)当∠B是直角时,因为∠C是直角,所以∠B+∠C=180°,与三角形的内角和定理矛盾.
(2)当∠B为钝角时,∠B+∠C>180°,同理矛盾.故___________,原命题成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
几何证明选讲
如图,在厶ABC中,![]() 为钝角,点是边AB上的点,点K和M分别
为钝角,点是边AB上的点,点K和M分别![]() 是边AC和BC上的点,且AH =AC,EB=BC,AE=AK,BH=BM.
是边AC和BC上的点,且AH =AC,EB=BC,AE=AK,BH=BM.
(I )求证:E、H、M、K四点共圆;
(II)若KE=EH,CE=3求线段 KM 的长.

查看答案和解析>>
科目:高中数学 来源: 题型:
选修4_1:(本小题满分10分)几何证明选讲如图,在厶ABC中,![]() 为钝角,点是边AB上的点,点K和M分别是边AC和BC上的点,且AH =AC,EB=BC,AE=AK,BH=BM.
为钝角,点是边AB上的点,点K和M分别是边AC和BC上的点,且AH =AC,EB=BC,AE=AK,BH=BM.
(I )求证:E、H、M、K四点共圆;
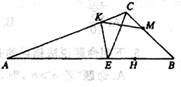 (II)若KE=EH,CE=3求线段 KM 的长.
(II)若KE=EH,CE=3求线段 KM 的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
选修4_1:(本小题满分10分)几何证明选讲如图,在厶ABC中,![]() 为钝角,点是边AB上的点,点K和M分别是边AC和BC上的点,且AH =AC,EB=BC,AE=AK,BH=BM.
为钝角,点是边AB上的点,点K和M分别是边AC和BC上的点,且AH =AC,EB=BC,AE=AK,BH=BM.
(I )求证:E、H、M、K四点共圆;
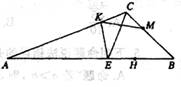 (II)若KE=EH,CE=3求线段 KM 的长.
(II)若KE=EH,CE=3求线段 KM 的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com