设数列{an}的前n项和为Sn,且满足Sn=2-an,n=1,2,3,….
(1)求数列{an}的通项公式;
(2)若数列{bn}满足b1=1,且bn+1=bn+an,求数列{bn}的通项公式;
(3)设cn=n (3-bn),求数列{cn}的前n项和为Tn.
【答案】
分析:(1)利用数列中a
n与 Sn关系
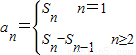
解决.
(2)结合(1)所求得出b
n+1-b
n=
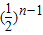
.利用累加法求b
n(3)由上求出c
n=n (3-b
n)=
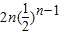
,利用错位相消法求和即可.
解答:解:(1)因为n=1时,a
1+S
1=a
1+a
1=2,所以a
1=1.
因为S
n=2-a
n,即a
n+S
n=2,所以a
n+1+S
n+1=2.
两式相减:a
n+1-a
n+S
n+1-S
n=0,即a
n+1-a
n+a
n+1=0,故有2a
n+1=a
n.
因为a
n≠0,所以
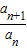
=

( n∈N
*).
所以数列{a
n}是首项a
1=1,公比为

的等比数列,a
n=
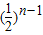
( n∈N
*).
(2)因为b
n+1=b
n+a
n( n=1,2,3,…),所以b
n+1-b
n=
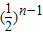
.从而有b
2-b
1=1,b
3-b
2=

,b
4-b
3=
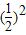
,…,b
n-b
n-1=
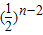
( n=2,3,…).
将这n-1个等式相加,得b
n-b
1=1+

+
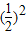
+…+
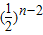
=
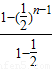
=2-

.
又因为b
1=1,所以b
n=3-
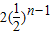
( n=1,2,3,…).
(3)因为c
n=n (3-b
n)=
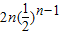
,
所以T
n=
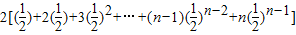
. ①
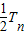
=
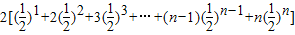
. ②
①-②,得
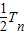
=
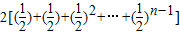
-
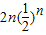
.
故T
n=
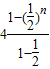
-
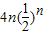
=8-
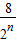
-
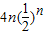
=8-
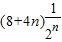
( n=1,2,3,…).
点评:本题考查利用数列中a
n与 Sn关系
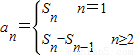
求数列通项,累加法、错位相消法求和,考查转化、变形构造、计算能力.

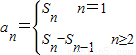 解决.
解决.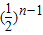 .利用累加法求bn
.利用累加法求bn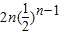 ,利用错位相消法求和即可.
,利用错位相消法求和即可.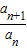 =
= ( n∈N*).
( n∈N*). 的等比数列,an=
的等比数列,an=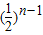 ( n∈N*).
( n∈N*).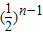 .从而有b2-b1=1,b3-b2=
.从而有b2-b1=1,b3-b2= ,b4-b3=
,b4-b3=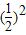 ,…,bn-bn-1=
,…,bn-bn-1=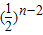 ( n=2,3,…).
( n=2,3,…). +
+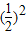 +…+
+…+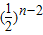 =
=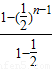 =2-
=2- .
.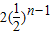 ( n=1,2,3,…).
( n=1,2,3,…).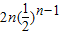 ,
,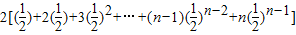 . ①
. ①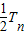 =
=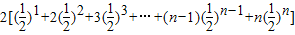 . ②
. ②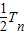 =
=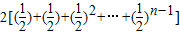 -
-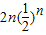 .
.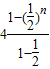 -
-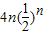 =8-
=8-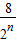 -
-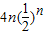 =8-
=8-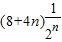 ( n=1,2,3,…).
( n=1,2,3,…).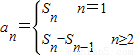 求数列通项,累加法、错位相消法求和,考查转化、变形构造、计算能力.
求数列通项,累加法、错位相消法求和,考查转化、变形构造、计算能力. 
