
(1)直线AB分别与平面α,B所成角的大小;
(2)二面角A1—AB—B1的大小.
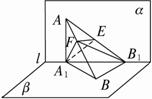
解:(1)如图,连结A1B,AB1.

∵α⊥B,α∩B=l,AA1⊥l,BB1⊥l,
∴AA1⊥B,BB1⊥α,
则∠BAB1,∠ABA1分别是AB与α和B所成的角.Rt△BB![]() ,AB=2.
,AB=2.
∴sinBAB1=![]() ,
,
∴∠BAB1=45°.
Rt△AA1B中,AA1=1,AB=2.
∴sinABA1=![]() .
.
∴∠ABA1=30°.
故AB与平面α,B所成的角分别是45°,30°.
(2)∵BB1⊥α,∴平面ABB1⊥α,在平面α内过A1作A1E⊥AB1交AB1于E,则A1E⊥平面AB1B,过E作EF⊥AB交AB于F,连结A
∴∠A1FE就是所求二面角的平面角.
在Rt△ABB1中,∠BAB1=45°,∴AB1=B1B=![]() .
.
在Rt△AA1B1中,AA1=A1B1=1,∴A1E=![]() AB1=
AB1=![]() .
.
在Rt△AA1B中,A1B=![]() .
.
由AA1·A1B=A![]() ,
,
∴在Rt△A1EF中,sinA1FE=![]() .
.
∴二面角A1—AB—B1的大小为arcsin![]() .
.


科目:高中数学 来源: 题型:
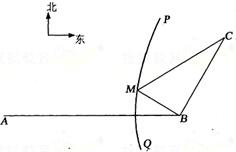 如图,B地在A地的正东方向4km处,C地在B地的北偏东30°方向2km处,河流
如图,B地在A地的正东方向4km处,C地在B地的北偏东30°方向2km处,河流A、(2
| ||
| B、5a万元 | ||
C、(2
| ||
D、(2
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,过抛物线x2=4y的对称轴上任一点P(0,m)(m>0)作直线与抛物线交于A(x1,y1),B(x2,y2)两点.
如图,过抛物线x2=4y的对称轴上任一点P(0,m)(m>0)作直线与抛物线交于A(x1,y1),B(x2,y2)两点.| AP |
| PB |
| x1 |
| x2 |
| QP |
| QA |
| QB |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (选做题)在A,B,C,D四小题中只能选做2题,每小题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
(选做题)在A,B,C,D四小题中只能选做2题,每小题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.| 3 |
| 3 |
|
| 2 |
| π |
| 4 |
|
| 1 |
| 2a |
| 1 |
| 2b |
| 1 |
| 2c |
| 1 |
| b+c |
| 1 |
| c+a |
| 1 |
| a+b |
查看答案和解析>>
科目:高中数学 来源: 题型:
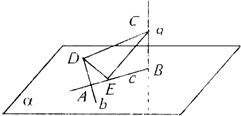 (2007•青岛一模)如图所示,b、c在平面α内,a∩c=B,b∩c=A,且a⊥b,a⊥c,b⊥c,若C∈a,D∈b,E在线段AB上(C,D,E均异于A,B),则△CDE是( )
(2007•青岛一模)如图所示,b、c在平面α内,a∩c=B,b∩c=A,且a⊥b,a⊥c,b⊥c,若C∈a,D∈b,E在线段AB上(C,D,E均异于A,B),则△CDE是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com