
过原点O作经过A(1,1),B(2,2)两点的圆的切线,则切点的轨迹是
4x2+y2=1(x≠y)
x2-y2=4(x≠y)
4y2+x2=1(x≠y)
x2+y2=4(x≠y)
|
分析一:若是选择、填空题可考虑选用几组特殊值代入求解. 解法一:如图,若AB为直径,C为圆心,过点O作该圆的切线,P(x,y)为切点.
因为点C为线段AB的中点,所以点C的坐标为 连接CP,则CP⊥OP. 所以OP2=OC2-CP2,即OP2=OC2-CA2. 所以x2+y2= 分析二:过点O作经过A,B两点的圆的切线,设P为切点,考虑PO是否为定值,若是,则点P的轨迹可确定. 解法二:过点O作经过A,B两点的圆的切线,设P为切点. 如图,连接AP.
因为两已知点的坐标分别为A(1,1),B(2,2), 所以O,A,B三点在同一直线上. 结合平面几何知识,可知∠OPA=∠B. 又因为∠AOP=∠BOP,所以△AOP∽△POB. 所以 所以OP2=OA·OB= 所以|OP|=2. 所以点P的轨迹是以O为圆心,2为半径长的圆(不包括( 分析三:由已知条件设法找到一几何等式,然后将其坐标化,即可得到切点的轨迹方程. 解法三:由解法二知,OP2=OA·OB.设点P的坐标为(x,y),将坐标代入,得x2+y2= 分析四:设P(x,y)为切点,C(a,b)为圆心,可先考虑将x,y,a,b联系起来,然后消去a,b即可得到点P的轨迹方程. 解法四:设P(x,y)为切点,C(a,b)为圆心,如图,则CP⊥OP.
所以OP2=OC2-CP2=OC2-CA2. 所以x2+y2=a2+b2-[(a-1)2+(b-1)2]=2(a+b)-2.(*) 因为两已知点的坐标分别为A(1,1),B(2,2), 所以线段AB的中点D的坐标为 所以线段AB的垂直平分线CD的方程为x+y-3=0. 把C(a,b)代入,得a+b-3=0,即a+b=3, 代入(*)式,得x2+y2=6-2=4(x≠y). 故选D. 点评:以上四种解法虽然有些解法用到的等式一样,但解法的本质是不一样的,希望同学们细心区分这四种解法的异同,领会其解题思想,掌握其解题方法,以便遇到轨迹题时可迅速选择一种较简捷的方法解答. |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源:内蒙古元宝山区一中2011届高三第一次摸底考试理科数学试题 题型:013
已知F1、F2分别为椭圆![]() =1(a>b>0)的左右焦点,经过椭圆上第二象限内任意一点P的切线为l,过原点O作OM∥l交F2P于点M,则|MP|与a、b的关系是
=1(a>b>0)的左右焦点,经过椭圆上第二象限内任意一点P的切线为l,过原点O作OM∥l交F2P于点M,则|MP|与a、b的关系是
|MP|=a
|MP|>a
|MP|=b
|MP|<b
查看答案和解析>>
科目:高中数学 来源:2010年内蒙古元宝山区高三第一次摸底考试理科数学卷 题型:选择题
已知F1、F2分别为椭圆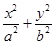 =1(a>b>0)的左右焦点,经过椭圆上第二象限内任意一点P的切线为l,过原点O作OM∥l交F2P于点M,则|MP|与a、b的关系是( )
=1(a>b>0)的左右焦点,经过椭圆上第二象限内任意一点P的切线为l,过原点O作OM∥l交F2P于点M,则|MP|与a、b的关系是( )
A.|MP|=a B.|MP|>a C.|MP|=b D.|MP|<b
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)求证:坐标原点O在圆C外;
(2)过点O作直线l,使直线l与⊙C在第一象限相切,求直线l与直线AC所成的角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com