
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源: 题型:
 如图,在△ABC中,设
如图,在△ABC中,设| AB |
| AC |
| AP |
| S平行四边形ANPM |
| S△ABC |
查看答案和解析>>
科目:高中数学 来源:2014届甘肃天水一中高二下学期期末考试文科数学试卷(解析版) 题型:填空题
已知边长分别为a、b、c的三角形ABC面积为S,内切圆O半径为r,连接OA、OB、OC,则三角形OAB、OBC、OAC的面积分别为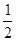 cr、
cr、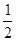 ar、
ar、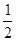 br,由S=
br,由S=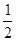 cr+
cr+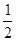 ar+
ar+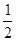 br得r=
br得r=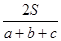 ,类比得若四面体的体积为V,四个面的面积分别为A、B、C、D,则内切球的半径R=_____________.
,类比得若四面体的体积为V,四个面的面积分别为A、B、C、D,则内切球的半径R=_____________.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省聊城市某重点高中高三(上)第二次调研数学试卷(理科)(解析版) 题型:解答题
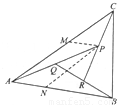
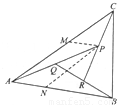
 ,
, ,AP的中点为Q,BQ的中点为R,CR的中点恰为P.
,AP的中点为Q,BQ的中点为R,CR的中点恰为P.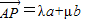 ,求λ和μ的值;
,求λ和μ的值; .
.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省池州一中高三(上)第三次月考数学试卷(文科)(解析版) 题型:解答题
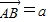 ,
,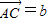 ,AP的中点为Q,BQ的中点为R,CR的中点恰为P.
,AP的中点为Q,BQ的中点为R,CR的中点恰为P.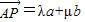 ,求λ和μ的值;
,求λ和μ的值;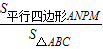 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com