
分析 由题意,关于x 的方程sinx+cosx-m=0在区间[0,$\frac{π}{2}$]上有解,转化为函数y=$\sqrt{2}$sin(x+$\frac{π}{4}$)与函数y=m的图象有交点问题.
解答 解:由题意,sinx+cosx-m=0,转化为:sinx+cosx=m,设函数y=$\sqrt{2}$sin(x+$\frac{π}{4}$)
x∈[0,$\frac{π}{2}$]上,则x+$\frac{π}{4}$∈[$\frac{π}{4}$,$\frac{3π}{4}$]
∴sin(x+$\frac{π}{4}$)∈[$\frac{\sqrt{2}}{2},1$]
∴函数y=$\sqrt{2}$sin(x+$\frac{π}{4}$)的值域为[1,$\sqrt{2}$]
关于x 的方程sinx+cosx-m=0在区间[0,$\frac{π}{2}$]上有解,
则函数y=m的值域为[1,$\sqrt{2}$],即m∈[1,$\sqrt{2}$]
故答案为:[1,$\sqrt{2}$].
点评 本题考查了方程有解问题转化为两个函数的交点的问题.属于基础题.


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源: 题型:解答题
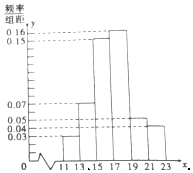 一企业从某生产线上随机抽取100件产品,测量这些产品的某项技术指标值x,得到的频率分布直方图如图.
一企业从某生产线上随机抽取100件产品,测量这些产品的某项技术指标值x,得到的频率分布直方图如图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -6 | B. | -2 | C. | -1 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ¬p:?x∈(1,+∞),x3+16≤8x | B. | ¬p:?x∈(1,+∞),x3+16<8x | ||
| C. | ¬p:?x0∈(1,+∞),x03+16≤8x0 | D. | ¬p:?x0∈(1,+∞),x03+16<8x0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,-2] | B. | [2,3] | C. | [-3,-2]∪{3} | D. | [2,3]∪{-3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 15 | B. | 9 | C. | 1 | D. | -$\frac{5}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com