
已知f(x)=Inx,g(x)=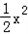 +mx+
+mx+ (m<0),直线l与函数f(x)的图象相切,切点的横坐标为1,且直线l与函数g(x)的图象也相切.
(m<0),直线l与函数f(x)的图象相切,切点的横坐标为1,且直线l与函数g(x)的图象也相切.
(1)求直线l的方程及实数m的值;
(2)若h(x)=f(x+1)﹣g′(x)(其中g′(x)是g(x)的导函数),求函数h(x)的最大值;
(3)当0<b<a时,求证:f(a+b)﹣f(2a)<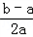 .
.
解:(1)∵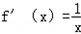 ,∴f'(1)=1.
,∴f'(1)=1.
∴直线l的斜率为1,且与函数f(x)的图象的切点坐标为(1,0).
∴直线l的方程为y=x﹣1.
又∵直线l与函数y=g(x)的图象相切,
∴方程组 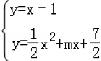 有一解.
有一解.
由上述方程消去y,并整理得x2+2(m﹣1)x+9=0 ①
依题意,方程①有两个相等的实数根,
∴△=[2(m﹣1)]2﹣4×9=0 解之,得m=4或m=﹣2
∵m<0,∴m=﹣2.
(2)由(1)可知 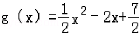 ,
,
∴g'(x)=x﹣2
∴h(x)=ln(x+1)﹣x+2(x>﹣1).
∴ 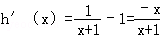
∴当x∈(﹣1,0)时,h'(x)>0,
当x∈(0,+∞)时,h'(x)<0.
∴当x=0时,h(x)取最大值,其最大值为2,
(3)f(a+b)﹣f(2a)=ln(a+b)﹣ln2a=ln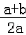 =ln(1+
=ln(1+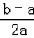 ).
).
∵0<b<a,
∴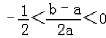 .
.
由(2)知当x∈(﹣1,0)时,h(x)<h(0)
∵当x∈(﹣1,0)时,ln(1+x)<x,ln(1+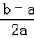 )<
)<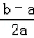 .
.
∴f(a+b)﹣f(2a)<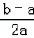


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:
| 1 |
| x |
| f(x2)-f(x1) |
| x2-x1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

 .请结合(I)中的结论证明x1<x3<x2.
.请结合(I)中的结论证明x1<x3<x2.查看答案和解析>>
科目:高中数学 来源:2002-2013学年江苏省泰州二中高二(下)期中数学试卷(理科)(解析版) 题型:解答题

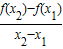 .请结合(I)中的结论证明x1<x3<x2.
.请结合(I)中的结论证明x1<x3<x2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com