Question

 

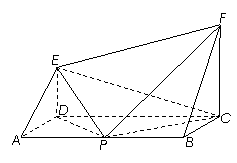
_{如图， ABCD为矩形，CF⊥平面ABCD，DE⊥平面ABCD，}

_{AB=4a，BC= CF=2a，DE=a， P为AB的中点.}

_{（1）求证：平面PCF⊥平面PDE；}

_{（2）求证：AE∥平面BCF.}

Answer 1

证明：（1）在矩形ABCD中，由AP=BP=BC=2a可得PC=PD=………………1分

又CD=4a，由勾股定理可得PD⊥PC……………………3分

因为CF⊥平面ABCD，则PD⊥CF……………………5分

由PCCF=C可得PD⊥平面PFC……………………6分

故平面PCF⊥平面PDE……………………7分

（2）作FC中点M，连接EM、BM

由CF⊥平面ABCD，DE⊥平面ABCD可得CM∥DE，又CM=DE=a，得四边形DEMC为平行四边形

故ME∥CD∥AB，且ME=D=AB，所以四边形AEMB为平行四边形故AE∥BM…………12分

又AE平面BCF，BM平面BCF，所以AE∥平面BCF. ……………………14分

注：本题也可以用平面ADE∥平面BCF证。