练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知如图所示，AB是⊙O中一条长为4的弦，P是⊙O上一动点，．问是否存在以A、P、B为顶点的面积最大的三角形，试说明理由；若存在，求出这个三角形的面积．
    答案：略
    解析：

    解：存在以A、P、B为顶点的面积最大的三角形．

    ∵，∴．

    ∴AB不是⊙O的直径，取中点P，作PD⊥AB于D，则PD为弓形高，且PD所在的直线必过圆心．

    ∵当点P在优弧上时，PD大于圆的半径，

    当点P在劣弧上时，PD小于⊙O的半径．

    ∴优弧与弦AB构成的弓形的弓高大于劣弧与弦AB构成的弓形的弓高．

    ∴点P必在优弧上，∵AB长为定值．

    ∴当点P为优弧中点时，△APB的面积最大，连结PA、PB．

    则等腰三角形APB即为所求，作⊙O的直径AC，连结BC．

    ∴∠ABC=90°，∠APB=∠C，∴．设BC=x，则AC=3x，在Rt△ABC中，AB=4，由勾股定理得，，

    ∴，得．

    ∴，，

    ∴．

    又∵AO=OC，AD=DB，

    ∴，

    ∴，

    ∴．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

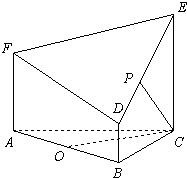    精英家教网如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得，已知FA⊥平面ABC，AB=2，BD=1，AF=2，CE=3，O为AB的中点．
    （Ⅰ）求平面DEF与平面ABC相交所成锐角二面角的余弦值；
    （Ⅱ）在DE上是否存在一点P，使CP⊥平面DEF？如果存在，求出DP的长；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知：如图所示的多面体是由底面为ABCD的长方体被截面AEGF所截得的，其中AB=4，BC=2，CG=3，BE=1，
    （1）求：BF与平面BCGE所成角的正切值
    （2）求：截面AEGF与平面ABCD所成的二面角的余弦值
    （3）在线段CG上是否存在一点M，使得M在平面AEGF上的射影恰为△EGF的重心．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得，已知FA⊥
    平面ABC，AB=2，AF=2，CE=3，BD=1，O为BC的中点．
    （1）求证：AO∥平面DEF；
    （2）求证：平面DEF⊥平面BCED；
    （3）求平面DEF与平面ABC相交所成锐角二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

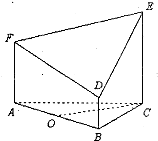    如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得，已知FA⊥平面ABC，BD=1，AF=2，CE=3，O为AB的中点．
    （1）求证：OC⊥DF；
    （2）试问线段CE上是否存在一点P，使得OP∥平面DEF？若存在，求出CP的长度，若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案