练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知f(x)=
    f(x-7)，x≥0
    log5(-x)，x＜0.
    则f(9)    等于（　　）
    分析：先将9代入解析式f（x-7）得到f（2），再将2代入f（x-7）得到f（-5），将-5代入解析式log5（-x）求出值．
    解答：解：因为f(x)=
    f(x-7)，x≥0
    log5(-x)，x＜0
    ，
    所以f（9）=f（9-7）=f（2）=f（2-7）=f（-5）=log55=1
    故选C．
    点评：本题考查求分段函数的函数值，关键是判断出自变量所属的段，然后将其代入相应段的解析式，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：全优设计选修数学－1-1苏教版 苏教版 题型：013

    已知f(x)＝ln|x|，则正确的命题是

    [　　]

    A．x＞0时，(x)＝；x＜0时，(x)＝－

    B．x＞0时，(x)＝，x＜0时，(x)不存在

    C．x≠0时，(x)＝

    D．由于x＝0无意义，则f(x)＝ln|x|不能求导

    查看答案和解析>>

    科目：高中数学 来源：湖南邵东二中2008届高三质量检测数学试题卷 题型：013

    已知f(x)是R上的减函数，且f(0)＝3，f(3)＝－1设P＝{x|f(x＋t)＜3}，Q＝{x|f(x)＜－1}若“x∈P”是“x∈Q”的充分不必要条件，则实数t的取值范围

    [　　]

    A．t＜－3

    B．t≥－3

    C．t＜0

    D．t≥0

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （09年西城区抽样理）（14分）

     已知f (x)、g(x)都是定义在R上的函数，如果存在实数m、n使得h (x) = m f(x)+ng(x)，那么称h (x)为f (x)、g(x)在R上生成的一个函数.

    设f (x)=x2+ax，g(x)=x+b(R)，l(x)= 2x2+3x-1，h (x)为f (x)、g(x)在R上生成的一个二次函数.

    （Ⅰ）设，若h (x)为偶函数，求；

    （Ⅱ）设，若h (x)同时也是g(x)、l(x) 在R上生成的一个函数，求a+b的最小值；

    （Ⅲ）试判断h(x)能否为任意的一个二次函数，并证明你的结论.

    查看答案和解析>>

    科目：高中数学 来源：2010年江苏省高二下学期期末考试数学卷 题型：解答题

    （本小题满分16分）

    已知f (x)、g(x)都是定义在R上的函数，如果存在实数m、n使得h (x) = m f(x)+ng(x)，那么称h (x)为f (x)、g(x)在R上生成的一个函数.

    设f (x)=x2+ax，g(x)=x+b(R)，= 2x2+3x-1，h (x)为f (x)、g(x)在R上生成的一个二次函数.

    （1）设，若h (x)为偶函数，求；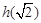

    （2）设，若h (x)同时也是g(x)、l(x) 在R上生成的一个函数，求a+b的最小值；

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知f(x)=x2+c,且f［f(x)］=f(x2+1)
    (1)设g(x)=f［f(x)］,求g(x)的解析式；
    (2)设φ(x)=g(x)-λf(x),试问:是否存在实数λ,使φ(x)在(-∞,-1)内为减函数，且在(-1，0)内是增函数

    查看答案和解析>>

    同步练习册答案