
分析 (1)讨论对称轴与区间的位置关系,判断f(x)的单调性,得出最大值,根据最大值列方程得出a或b的关系及范围,从而得出a2+|b|的取值范围;
(2)讨论对称轴与区间的位置关系,计算f(x)的最值,及a,b的关系,将结论转化为证明$\frac{1}{2}$(|a-2b|+a)-|fmax(x)|≥0且$\frac{1}{2}$(|a-2b|+a)-|fmin(x)|≥0.
解答 解:(1)∵a>0,∴f(x)的图象开口向上,对称轴为直线x=$\frac{a+b}{3a}$,
令z=a2+|b|,
①若$\frac{a+b}{3a}$>$\frac{1}{2}$,即2b≥a>0时,fmax(x)=f(0)=b=1,∴0<a≤2,
∴a2+|b|=a2+1
∴1<z≤5.
②若$\frac{a+b}{3a}$≤$\frac{1}{2}$,即2b≤a时,fmax(x)=f(1)=a-b=1,∴b=a-1,
∴2a-2≤a,即0<a≤2
∴|b|=|a-1|=$\left\{\begin{array}{l}{a-1,0<a≤1}\\{1-a,1<a≤2}\end{array}\right.$,
z=a2+|b|=$\left\{\begin{array}{l}{{a}^{2}+a-1,0<a≤1}\\{{a}^{2}-a+1,1<a≤2}\end{array}\right.$.
∴z(a)=a2+|b|在(0,1]上单调递增,在(1,2]上单调递增,
∴-1<z≤1或1<z≤3.
综上,a2+|b|的取值范围是(-1,5].
(2)①若$\frac{a+b}{3a}≤0$,即b≤-a时,f(x)在[0,1]上单调递增,
∴fmax(x)=f(1)=a-b>0,fmin(x)=f(0)=b<0,
∵b≤-a,∴|a-2b|=a-2b,
∴$\frac{1}{2}$(|a-2b|+a)-|fmax(x)|=a-b-(a-b)=0,
$\frac{1}{2}$(|a-2b|+a)-|fmin(x)|=a-b-(-b)=a>0,
∴$\frac{1}{2}$(|a-2b|+a)≥|f(x)|.
②若$\frac{a+b}{3a}≥1$,即b≥2a时,f(x)在[0,1]上单调递减,
fmax(x)=f(0)=b>0,fmin(x)=f(1)=a-b<0,
∵b≥2a,∴|a-2b|=2b-a,
∴$\frac{1}{2}$(|a-2b|+a)-|fmax(x)|=b-b=0,
$\frac{1}{2}$(|a-2b|+a)-|fmin(x)|=b-(b-a)=a>0,
$\frac{1}{2}$(|a-2b|+a)≥|f(x)|.
③若0<$\frac{a+b}{3a}$≤$\frac{1}{2}$,即-a<b≤-$\frac{1}{2}$a时,f(x)在[0,1]上先减后增,
∴fmin(x)=f($\frac{a+b}{3a}$)=-$\frac{{a}^{2}+{b}^{2}-ab}{3a}$,fmax(x)=f(1)=a-b>0,
此时,|a-2b|=a-2b,fmin(x)<0,
∴$\frac{1}{2}$(|a-2b|+a)-|fmax(x)|=a-b-(a-b)=0,
$\frac{1}{2}$(|a-2b|+a)-|fmin(x)|=a-b-$\frac{{a}^{2}+{b}^{2}-ab}{3a}$=$\frac{2{a}^{2}-{b}^{2}-2ab}{3a}$,
∵-a<b≤-$\frac{1}{2}$a,∴2a2-b2>a2>0,-2ab>0,
∴$\frac{1}{2}$(|a-2b|+a)-|fmin(x)|>0,
∴$\frac{1}{2}$(|a-2b|+a)≥|f(x)|.
④若$\frac{1}{2}$<$\frac{a+b}{3a}$<1,即$\frac{a}{2}<b<2a$时,f(x)在[0,1]上先减后增,
fmin(x)=f($\frac{a+b}{3a}$)=-$\frac{{a}^{2}+{b}^{2}-ab}{3a}$,fmax(x)=f(0)=b>0
∵$\frac{a}{2}<b<2a$,∴a2+b2-ab≥2ab-ab=ab>0,∴fmin(x)<0.
此时,|a-2b|=2b-a,
∴$\frac{1}{2}$(|a-2b|+a)-|fmax(x)|=b-b=0,
$\frac{1}{2}$(|a-2b|+a)-|fmin(x)|=b-$\frac{{a}^{2}+{b}^{2}-ab}{3a}$=$\frac{4ab-{a}^{2}-{b}^{2}}{3a}$=$\frac{2ab-(a-b)^{2}}{3a}$,
∵$\frac{a}{2}<b<2a$,∴2ab>a2,-a<a-b<$\frac{a}{2}$,∴(a-b)2<a2,
∴$\frac{1}{2}$(|a-2b|+a)-|fmin(x)|>0,
∴$\frac{1}{2}$(|a-2b|+a)≥|f(x)|.
综上,$\frac{1}{2}$(|a-2b|+a)≥|f(x)|.
∴|f(x)|≤$\frac{1}{2}$(|a-2b|+a).
点评 本题考查了二次函数的单调性与最值计算,不等式的性质,分类讨论思想,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (0,1] | C. | (-1,1) | D. | (-1,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}-\frac{3}{2}i$ | B. | $\frac{1}{2}+\frac{3}{2}i$ | C. | 1+3i | D. | 1-3i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,1] | B. | [0,$\sqrt{2}$] | C. | [$-\sqrt{2}$,$\sqrt{2}$] | D. | [-2,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
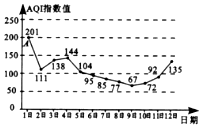 AQI是表示空气质量的指数,AQI指数值越小,表明空气质量越好,当AQI指数值不大于100时称空气质量为“优良”.如图是某地4月1日到12日AQI指数值的统计数据,图中点A表示4月1日的AQI指数值为201,则下列叙述不正确的是( )
AQI是表示空气质量的指数,AQI指数值越小,表明空气质量越好,当AQI指数值不大于100时称空气质量为“优良”.如图是某地4月1日到12日AQI指数值的统计数据,图中点A表示4月1日的AQI指数值为201,则下列叙述不正确的是( )| A. | 这12天中有6天空气质量为“优良” | B. | 这12天中空气质量最好的是4月9日 | ||
| C. | 这12天的AQI指数值的中位数是90 | D. | 从4日到9日,空气质量越来越好 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 必要不充分条件 | B. | 既不充分也不必要条件 | ||
| C. | 充要条件 | D. | 充分不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com