x
分析:函数对于n∈N
*,通过定义f
n+1(x)=f
1[f
n(x)],求出f
2(x)=f
1[f
1(x)].f
3(x),f
4(x),f
5(x),f
6(x),f
7(x).所以从f
1(x)到f
6(x),每6个一循环.由此能求出结果.
解答:∵函数对于n∈N
*,定义f
n+1(x)=f
1[f
n(x)],
∴f
2(x)=f
1[f
1(x)]=f
1(
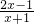
)=

=

.
f
3(x)=f
1[f
2(x)]=f
1(

)=

=

,
f
4(x)=f
1[f
3(x)]=f
1(

)=

=

,
f
5(x)=f
1[f
4(x)]=f
1(

)=

=

,
f
6(x)=f
1[f
5(x)]=f
1(

)=

=x,
f
7(x)=f
1[f
6(x)]=f
1(x)=
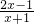
=f
1(x).
所以从f
1(x)到f
6(x),每6个一循环.
∵60=10×6,
∴f
60(x)=f
6(x)=x,
故答案为:x.
点评:本题考查函数的周期性,函数值的求法,是基础题.解题时要认真审题,解题的关键是:得到从f
1(x)到f
6(x),求出函数值的周期.

 ,
, ,则f60(x)=________.
,则f60(x)=________.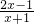 )=
)= =
= .
. )=
)= =
= ,
, )=
)= =
= ,
, )=
)= =
= ,
, )=
)= =x,
=x,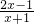 =f1(x).
=f1(x).
