
 =(
=( x,x-4),向量
x,x-4),向量 =(x,
=(x, x),x∈[-4,5]
x),x∈[-4,5] •
• ;
;  •
• 的最大值,并求此时的cos<
的最大值,并求此时的cos< 、
、 >.(<
>.(< 、
、 >表示两向量的夹角)
>表示两向量的夹角) •
• =2x2-6x-----------------------------------------(3分)
=2x2-6x-----------------------------------------(3分) )2-
)2- ,
, •
• 的最大值为56--------------------------------------(9分)
的最大值为56--------------------------------------(9分) =(-2,-8),
=(-2,-8), =(-4,-6),|
=(-4,-6),| |=
|=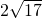 ,|
,| |=2
|=2
 、
、 的夹角为θ,则cosθ=
的夹角为θ,则cosθ= .------------------(12分)
.------------------(12分) •
• 的表达式即可;
的表达式即可;  •
• 的表达式,通过二次函数求出最大值,求出此时的cos<
的表达式,通过二次函数求出最大值,求出此时的cos< ,
, >的值.
>的值.

 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:
| a |
| 3 |
| b |
| a |
| b |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| 3 |
| a |
| b |
| 5π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| m |
| π |
| 6 |
| n |
| m |
| n |
| 5π |
| 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
| 2f(θ)+f(x) |
| 3 |
| 2θ+x |
| 3 |
查看答案和解析>>
科目:高中数学 来源:南通高考密卷·数学(理) 题型:044
已知向量p=(a,x+1),q=(x,a),m=(1,y),且(p-q)∥m,y与x的函数关系式为y=f(x).
(1)求f(x);
(2)判断并证明函数y=f(x)当x>a时的单调性;
(3)我们利用函数y=f(x)构造一个数列{xn),方法如下:对于f(x)定义域中的x1,令x2=f(x1),x3=f(x2),…,xn=f(xn-1),….在上述构造数列的过程中,如果xi(i=1,2,3,4,…)在定义域中,构造数列的过程将继续下去;如果xi不在定义域中,则构造数列的过程停止.如果取f(x)定义域中任一值作为x1,都可以用上述方法构造出一个无穷数列{xn},求实数a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com