
若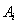 (
(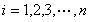 )是
)是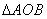 所在的平面内的点,且
所在的平面内的点,且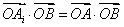 .
.
给出下列说法:①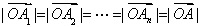 ;②
;②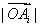 的最小值一定是
的最小值一定是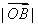 ;
;
③点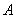 、
、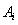 在一条直线上.其中正确的个数是( )
在一条直线上.其中正确的个数是( )
A.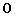 个. B.
个. B.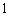 个. C.
个. C.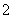 个. D.
个. D.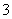 个.
个.
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源:2013-2014学年上海市普陀区高三上学期12月月考理科数学试卷(解析版) 题型:选择题
若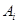 (
(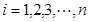 )是
)是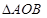 所在的平面内的点,且
所在的平面内的点,且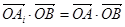 .
.
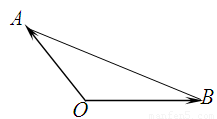
给出下列说法:
①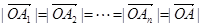 ;
;
②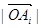 的最小值一定是
的最小值一定是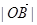 ;
;
③点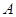 、
、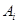 在一条直线上;
在一条直线上;
④向量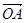 及
及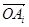 在向量
在向量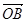 的方向上的投影必相等.
的方向上的投影必相等.
其中正确的个数是( )
A.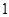 个. B.
个. B.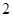 个.
C.
个.
C.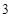 个.
D.
个.
D.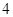 个.
个.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年上海市普陀区高三上学期12月月考文科数学试卷(解析版) 题型:选择题
若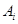 (
(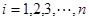 )是
)是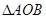 所在的平面内的点,且
所在的平面内的点,且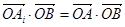 .
.
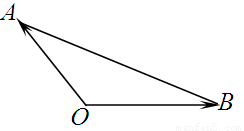
给出下列说法:
①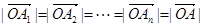 ;
;
②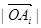 的最小值一定是
的最小值一定是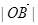 ;
;
③点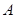 、
、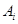 在一条直线上;
在一条直线上;
④向量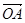 及
及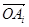 在向量
在向量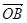 的方向上的投影必相等.
的方向上的投影必相等.
其中正确的个数是( )
A. 个. B.
个. B.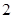 个.
C.
个.
C.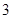 个.
D.
个.
D.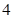 个.
个.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年四川省高三3月月考理科数学试卷 题型:填空题
给出下列命题,其中正确的命题是 (写出所有正确命题的编号).
①在 中,若
中,若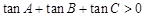 ,则
,则 是锐角三角形;
是锐角三角形;
②在 中,
中, 是
是 的充要条件;
的充要条件;
③已知非零向量 ,则“
,则“ ”是“
”是“ 的夹角为锐角”的充要条件;
的夹角为锐角”的充要条件;
④命题“在三棱锥 中,已知
中,已知 ,若点
,若点 在
在 所在的平面内,则
所在的平面内,则 ”的否命题为真命题;
”的否命题为真命题;
⑤函数 的导函数为
的导函数为 ,若对于定义域内任意
,若对于定义域内任意 ,
,
 ,有
,有 恒成立,则称
恒成立,则称 为恒均变函数,那么
为恒均变函数,那么 为恒均变函数
为恒均变函数
查看答案和解析>>
科目:高中数学 来源: 题型:
给出下列命题,其中正确的命题是 (写出所有正确命题的编号).
① 非零向量![]() 满足
满足![]() ,则
,则![]() 与
与![]() 的夹角为
的夹角为![]() ;
;
② 已知非零向量![]() ,则“
,则“![]() ”是“
”是“![]() 的夹角为锐角”的充要条件;
的夹角为锐角”的充要条件;
③ 命题“在三棱锥![]() 中,已知
中,已知![]() ,若点
,若点![]() 在
在![]() 所在的平面内,则
所在的平面内,则![]() ”的否命题为真命题;
”的否命题为真命题;
④ 若![]() ,则
,则![]() 为等腰三角形.
为等腰三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com