
设等差数列 的前n项和为
的前n项和为 ,已知
,已知 ,
, ,
, .
.
(1)求公差d的取值范围.
(2)指出 ,
, ,…,
,…, 中哪一个值最大,并说明理由.
中哪一个值最大,并说明理由.
|
解: (1)依题意有
由  ,得 ,得 . .
又  . .
(2) 解法1:由d<0,可知 . .
因此,若在 1≤n≤12中,存在自然数n,使得 , , ,则 ,则 就是 就是 , , ,…, ,…, 中的最大值. 中的最大值.
由于  , , ,即 ,即 , , ,由此得 ,由此得 . .
故在  , , ,…, ,…, 中 中 的值最大. 的值最大.
解法 2:
= 
∵ d<0,∴ 最小时, 最小时, 最大. 最大.
当  时, 时, . .
∴ n=6时, 最小 最小
∴  最大. 最大.
解法 3:由d<0,可知 .因此,若在 .因此,若在 中,存在自然数n,使得 中,存在自然数n,使得 , , ,则 ,则 就是 就是 , , ,…, ,…, 中的最大值. 中的最大值.
由已知 
故在  , , ,…, ,…, 中 中 的值最大. 的值最大.
|
|
本题考查数列、不等式及综合运用有关知识解决问题的能力. 第 (2)题用了三种方法来解,解法1与解法3类似,只是确定 、 、 的方法不同,解法1技巧性强,解法2是把问题转化成了有限制条件的一元二次函数最值问题. 的方法不同,解法1技巧性强,解法2是把问题转化成了有限制条件的一元二次函数最值问题. |


科目:高中数学 来源:2011-2012学年山东省菏泽市高三5月高考冲刺题文科数学试卷(解析版) 题型:选择题
设等差数列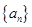 的前n项和为
的前n项和为 ,若
,若 ,
, ,则当
,则当 取最小值时,n等于
取最小值时,n等于
A.6 B.7 C.8 D.9
查看答案和解析>>
科目:高中数学 来源:2010年浙江省高一第二学期期中考试数学试题 题型:解答题
(本小题满分8分)
设等差数列 的前n项和为
的前n项和为 ,且
,且 (c是常数,
(c是常数,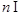 N*),
N*), .
.
(1)求c的值及 的通项公式;
的通项公式;
(2)证明: .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com